Question

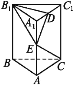
【题目】如图,在直三棱柱ABC-A1B1C1中,∠ABC=,D是棱AC的中点,且AB=BC=BB1=2.

(1)求证:AB1∥平面BC1D;

(2)求异面直线AB1与BC1所成的角.

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）连接B1C交BC1于点O,连接OD.利用三角形中位线说明OD∥AB1即得证。

（2）建立空间坐标系，求出=(0,-2,2),=(2,0,2).代入夹角计算公式即可。

(1)证明如图,连接B1C交BC1于点O,连接OD.

因为O为B1C的中点,D为AC的中点,所以OD∥AB1.

因为AB1平面BC1D,OD平面BC1D,

所以AB1∥平面BC1D.

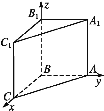
(2)解建立如图所示的空间直角坐标系Bxyz,

则B(0,0,0),A(0,2,0),C1(2,0,2),B1(0,0,2),

因此=(0,-2,2),=(2,0,2).

所以cos<>==,

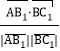设异面直线AB1与BC1所成的角为θ,则cos θ=,由于θ∈,故θ=.