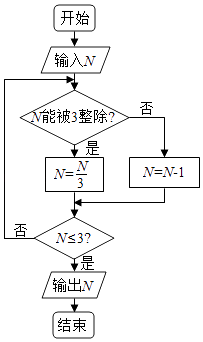
题目内容
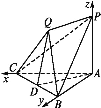
【题目】如图,在三棱锥P-ABC中,PA⊥底面ABC,△ABC是直角三角形,且PA=AB=AC.又平面QBC垂直于底面ABC.
(1)求证:PA∥平面QBC;
(2)若PQ⊥平面QBC,求锐二面角Q-PB-A的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)过点Q作QD⊥BC交BC于点D,则QD⊥平面ABC,而PA⊥平面ABC,可得QD∥PA,从而问题得证。
(2)建立空间直角坐标系,找出二面角Q-PB-A所在的两个平面的法向量,求出法向量夹角的余弦值,结合角的范围,得出最终结果。
(1)证明过点Q作QD⊥BC交BC于点D,
因为平面QBC⊥平面ABC,
所以QD⊥平面ABC.
又PA⊥平面ABC,
所以QD∥PA.
而QD平面QBC,PA平面QBC,
所以PA∥平面QBC.
(2)解因为PQ⊥平面QBC,
所以∠PQB=∠PQC=90°.
又PB=PC,PQ=PQ,
所以△PQB≌△PQC,
所以BQ=CQ.
所以点D是BC的中点,连接AD,则AD⊥BC,因此AD⊥平面QBC,故四边形PADQ是矩形.
分别以AC,AB,AP所在直线为x,y,z轴,建立如图所示的空间直角坐标系.
设PA=2a,则Q(a,a,2a),B(0,2a,0),P(0,0,2a).
设平面QPB的法向量为n=(x,y,z),
因为![]() =(a,a,0),
=(a,a,0),![]() =(0,2a,-2a),
=(0,2a,-2a),
所以![]()
取n=(1,-1,-1).
又平面PAB的一个法向量为m=![]() =(1,0,0),
=(1,0,0),
设锐二面角Q-PB-A的大小为θ,
则cos θ=|cos<m,n>|=![]() ,
,
即锐二面角Q-PB-A的余弦值等于![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目