Question

【题目】如图，圆的半径垂直于直径， 为上一点， 的延长线交圆于点，过点的切线交的延长线于点，连接.

（1）求证： ；

（2）若， ，求的长.

Answer 1

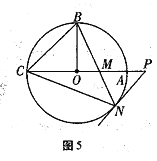
【答案】(1)证明见解析；(2)1.

【解析】试题分析：

(1)连接ON，由题意结合弦切角定理即可证得题中的结论；

(2)解法一：由题意结合相交弦定理可求得外接圆半径，则.

解法二：由题意结合正弦定理求得外接圆半径，则.

解法三：由题意得到关于圆的半径的方程，解方程可得半径，则.

试题解析：

（1）证明：连接，

∵为的切线，∴90°，

在中，∵，

∴，又∵，

∴，

根据弦切角定理，得，∴.

（2）解法一：∵，

∴为等边三角形，∴.

设的半径为，

则在直角三角形中，，，，

根据相交弦定理，，

可得，

即可得，，

∴.

解法二：∵60°，

∴△PMN为等边三角形，∴，

设的半径为r，则在直角三角形中，，，，

又为的外接圆，

由正弦定理可知，，

又，

∴，∴.

解法三：，

设的半径为r，则在直角三角形中，，，，

在中，，∴，

又∵，MN=PM=1，

∴，∴，∴.