题目内容
(本小题满分14分)
如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点, 截面DEF∥底面ABC, 且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)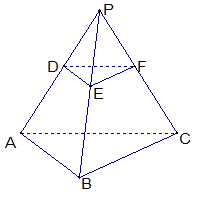
(1)求证:P-ABC为正四面体;
(2)棱PA上是否存在一点M,使得BM与面ABC所成的角为45°?若存在,求出点M的位置;若不存在,请说明理由。
(3)设棱台DEF-ABC的体积为V=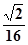 , 是否存在体积为V且各棱长均相等的平行六面体,使得它与棱台DEF-ABC有相同的棱长和,并且该平行六面体的一条侧棱与底面两条棱所成的角均为60°? 若存在,请具体构造出这样的一个平行六面体,并给出证明;若不存在,请说明理由.
, 是否存在体积为V且各棱长均相等的平行六面体,使得它与棱台DEF-ABC有相同的棱长和,并且该平行六面体的一条侧棱与底面两条棱所成的角均为60°? 若存在,请具体构造出这样的一个平行六面体,并给出证明;若不存在,请说明理由.
(1)见解析 (2)M点 满足AM=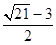
(3)构造棱长均为 ,底面为正方形或锐角为60°的菱形的平行六面体
,底面为正方形或锐角为60°的菱形的平行六面体
解析试题分析: 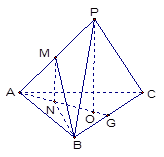
(1)解:∵棱台DEF-ABC与棱锥P-ABC的棱长和相等
∴DE+EF+FD=PD+OE+PF. 2分
又∵截面DEF∥底面ABC,
∴DE=EF=FD=PD=OE=PF,∠DPE=∠EPF=∠FPD=60°
∴P-ABC是正四面体. 4分
(2)(5分)
作PO⊥面ABC于O,MN⊥面ABC于N,
∵A、M、P三点共线 ∴A、N、O三点共线,延长AO交BC于G
∴∠MBN=45°,MN//PO
∵P-ABC为棱长为1的正四面体
∴ AO= ,PO=
,PO=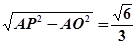 6分
6分
设MN=x,则BN=x,且
∴AM=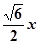 ,AN=
,AN=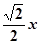
∵AG是等边△ABC的中线 ∴∠BAN=30°
∴BN2=AN2+AB2-2AB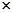 AN
AN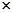 cos30° 8分
cos30° 8分
解得x=
∴AM=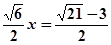 9分
9分
(3)(5分)
存在满足条件的平行六面体. 10分
棱台DEF-ABC的棱长和为定值6,则平行六面体的棱长均为 , 11分
, 11分
设该六面体一条侧棱长为A1B1,与底面两条棱A1C1和A1D1的夹角为60°,设底面四边形的锐角为2α, 作B1E1⊥底面A1C1D1于E1,E1F1⊥A1C1
∵∠B1A1C1=∠B1A1D1
∴∠C1A1E1=α
则A1F1=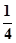 ,A1E1=
,A1E1=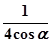 ,zxxk
,zxxk
B1E1=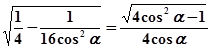
则V=
解得 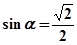 或
或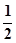
∴2α=90°或60° 13分
故构造棱长均为 ,底面为正方形或锐角为60°的菱形的平行六面体即满足要求. 14分
,底面为正方形或锐角为60°的菱形的平行六面体即满足要求. 14分
考点:棱柱 棱台的性质,直线与平面所成角,解三角形,柱体体积公式
点评:该题综合性较强,涉及多知识点的交汇

 综合自测系列答案
综合自测系列答案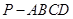 的底面
的底面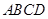 是菱形,
是菱形,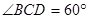 ,
,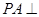 面
面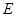 是
是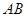 的中点,
的中点, 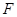 是
是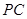 的中点.
的中点.
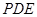 ⊥面
⊥面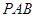 ;
; 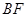 ∥面
∥面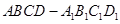 中,
中,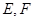 分别是
分别是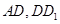 的中点,
的中点,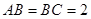 ,
,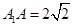 .
.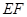 //平面
//平面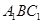 ;
;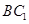 上是否存在点
上是否存在点 ,使直线
,使直线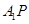 与
与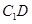 垂直,
垂直,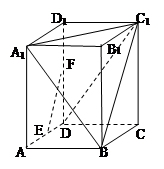
 是矩形,
是矩形, 平面
平面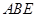 ,
,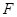 是
是 上一点,
上一点, 平面
平面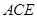 ,点
,点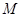 ,
, 分别是
分别是 的中点.
的中点. 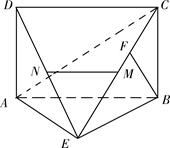
 平面
平面 .
.  平面
平面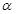 ,
,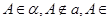 直线
直线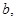
 ,则
,则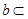 平面
平面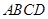 中,
中, ∥
∥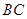 ,
,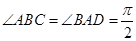 ,
,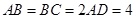 ,
,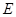 、
、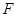 分别是
分别是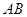 、
、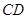 上的点,
上的点,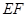 ∥
∥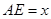 ,
,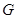 是
是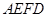 ⊥平面
⊥平面 (如图).
(如图).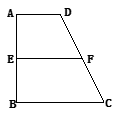
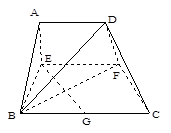
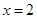 时,求证:
时,求证: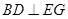 ;
;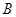 、
、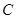 、
、 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为 ,求
,求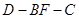 的余弦值.
的余弦值. BE,AB
BE,AB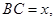
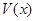 表示三棱锥B-ACE 的体积,求
表示三棱锥B-ACE 的体积,求