题目内容
把下面的符号语言改写成文字语言的形式,并画出图形。若直线 平面
平面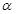 ,
,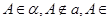 直线
直线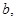
 ,则
,则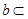 平面
平面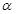
(理)若直线a在平面 内,点A也在平面
内,点A也在平面 内,但A不在直线a上,A在直线b上,a平行于b,则b在
内,但A不在直线a上,A在直线b上,a平行于b,则b在 内。
内。
解析

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
题目内容
把下面的符号语言改写成文字语言的形式,并画出图形。若直线 平面
平面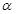 ,
,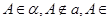 直线
直线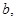
 ,则
,则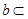 平面
平面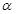
(理)若直线a在平面 内,点A也在平面
内,点A也在平面 内,但A不在直线a上,A在直线b上,a平行于b,则b在
内,但A不在直线a上,A在直线b上,a平行于b,则b在 内。
内。
解析

 习题精选系列答案
习题精选系列答案