题目内容
定义在R上的单调递减函数y=f(x)满足f(1-x)=-f(1+x),且对于任意x,y∈R,不等f(x2-2x)+f(y2-2y)≥0恒成立,则当x≥1时,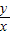 的取值范围为 .
的取值范围为 .
【答案】分析:先根据函数f(x)的性质化简不等式f(x2-2x)+f(y2-2y)≥0,得到关于x,y的约束条件,画出约束条件 的可行域,然后分析  的几何意义,结合图象,用数形结合的思想,即可求解.
的几何意义,结合图象,用数形结合的思想,即可求解.
解答: 解:∵f(1-x)=-f(1+x),
解:∵f(1-x)=-f(1+x),
∴f(2-x)=-f(x),
又∵f(x2-2x)+f(y2-2y)≥0
∴f(x2-2x)≥-f(y2-2y)
∴f(x2-2x)≥f(2-y2+2y)
∵定义在R上的单调递减函数y=f(x)
∴x2-2x≤2-y2+2y
即(x-1)2+(y-1)2≤4,表示一个圆,又x≥1
如下图所示:
又∵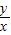 表示的是可行域内一点与原点连线的斜率
表示的是可行域内一点与原点连线的斜率
当x=1,y=3时, 有最大值 3;
有最大值 3;
当x=1,y=-1时,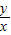 有最小值-1
有最小值-1
故答案为:[-1,3]
点评:平面区域的最值问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,分析表达式的几何意义,然后结合数形结合的思想,分析图形,找出满足条件的点的坐标,即可求出答案.
 的几何意义,结合图象,用数形结合的思想,即可求解.
的几何意义,结合图象,用数形结合的思想,即可求解.解答:
 解:∵f(1-x)=-f(1+x),
解:∵f(1-x)=-f(1+x),∴f(2-x)=-f(x),
又∵f(x2-2x)+f(y2-2y)≥0
∴f(x2-2x)≥-f(y2-2y)
∴f(x2-2x)≥f(2-y2+2y)
∵定义在R上的单调递减函数y=f(x)
∴x2-2x≤2-y2+2y
即(x-1)2+(y-1)2≤4,表示一个圆,又x≥1
如下图所示:
又∵
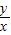 表示的是可行域内一点与原点连线的斜率
表示的是可行域内一点与原点连线的斜率当x=1,y=3时,
 有最大值 3;
有最大值 3;当x=1,y=-1时,
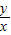 有最小值-1
有最小值-1故答案为:[-1,3]
点评:平面区域的最值问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,分析表达式的几何意义,然后结合数形结合的思想,分析图形,找出满足条件的点的坐标,即可求出答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (n∈N*).
(n∈N*).