题目内容
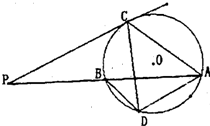（2011•洛阳二模）如图，已知PBA是圆O的割线，PC是圆的切线，C为切点，过点A引AD∥PC，交圆于D点，连接CD，BD，CA．
求证：
（1）CD=CA；
（2）CD2=PA•BD．
分析：（1）利用AD∥PC，PC是圆的切线，证明∠PCD=∠CAD，即可得到结论；
（2）证明△PCA∽△CBD，利用CD=CA，可得CD2=PA•BD．
（2）证明△PCA∽△CBD，利用CD=CA，可得CD2=PA•BD．
解答：证明：（1）∵AD∥PC，∴∠PCD=∠CDA，
∵PC是圆的切线，∴∠PCD是弦切角
∴∠PCD=∠CAD，∴CD=CA；
（2）连接BC，则∠BCD=∠BAD
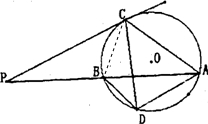
∵AD∥PC，∴∠P=∠DAB，
∴∠P=∠BCD
∴△PCA∽△CBD
∴
=
∵AC=CD
∴
=
∴CD2=PA•BD．
∵PC是圆的切线，∴∠PCD是弦切角
∴∠PCD=∠CAD，∴CD=CA；
（2）连接BC，则∠BCD=∠BAD
∵AD∥PC，∴∠P=∠DAB，
∴∠P=∠BCD
∴△PCA∽△CBD
∴
| BD |
| AC |
| CD |
| PA |
∵AC=CD
∴
| BD |
| CD |
| CD |
| PA |
∴CD2=PA•BD．
点评：本题考查圆的切线性质，与圆有关的三角形相似的判断，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目