题目内容
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
A.(不等式选做题)若不等式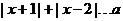 对任意
对任意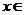 R恒成立,则
R恒成立,则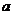 的取值范围是
.
的取值范围是
.
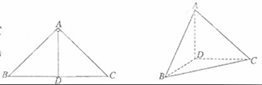
B.(几何证明选做题)如图,∠B=∠D,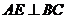 ,
,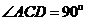 ,且AB=6,AC=4,AD=12,则AE= .
,且AB=6,AC=4,AD=12,则AE= .
C.(坐标系与参数方程选做题)直角坐标系 中,以原点O为极点,
中,以原点O为极点,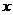 轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线
轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线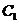 :
: (
(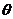 为参数)和曲线
为参数)和曲线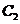 :
: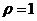 上,则
上,则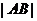 的最小值为
.
的最小值为
.
【答案】
A.【分析】先确定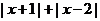 的取值范围,则只要
的取值范围,则只要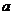 不大于
不大于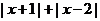 的最小值即可.
的最小值即可.
【解】当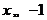 时,
时, ;
;
当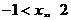 时,
时,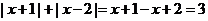 ;
;
当 时,
时,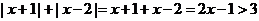 ;
;
综上可得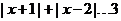 ,所以只要
,所以只要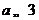 ,
,
即实数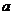 的取值范围是
的取值范围是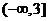 .
.
【答案】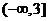
B.【分析】寻找两个三角形相似的条件,再根据相似三角形的对应边成比例求解.
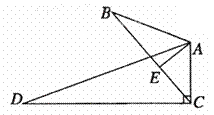
【解】因为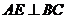 ,
,
所以∠AEB=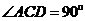 ,又因为∠B=∠D,所以△AEB∽△ACD,所以
,又因为∠B=∠D,所以△AEB∽△ACD,所以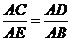 ,所以
,所以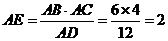 .
.
【答案】2
C.【分析】利用化归思想和数形结合法,把两条曲线转化为直角坐标系下的方程.
【解】曲线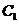 的方程是
的方程是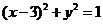 ,曲线
,曲线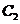 的方程是
的方程是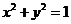 ,两圆外离,所以
,两圆外离,所以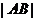 的最小值为
的最小值为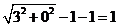 .
.
【答案】1

练习册系列答案
相关题目
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)