题目内容
已知数列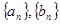 满足:
满足: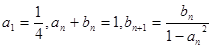
1)求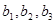 的值; 2)求证数列
的值; 2)求证数列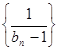 是等差数列,并求数列
是等差数列,并求数列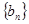 的通项公式;
的通项公式;
3)设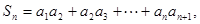 若
若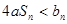 恒成立,求实数
恒成立,求实数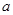 的取值范围.
的取值范围.
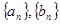 满足:
满足: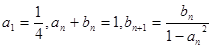
1)求
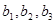 的值; 2)求证数列
的值; 2)求证数列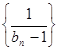 是等差数列,并求数列
是等差数列,并求数列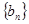 的通项公式;
的通项公式;3)设
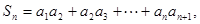 若
若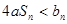 恒成立,求实数
恒成立,求实数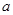 的取值范围.
的取值范围.解:(1) ∵ ∴
∴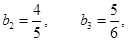
(2) ; (3)
; (3)  .
.
 ∴
∴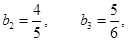
(2)
 ; (3)
; (3)  .
. 第一问中,利用 ,递推关系得到,
,递推关系得到,
∵ ∴
∴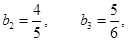
第二问中,∵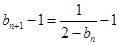 ∴
∴
∴数列{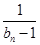 }是以-4为首项,-1为公差的等差数列。∴
}是以-4为首项,-1为公差的等差数列。∴
第三问中, ……………8分
……………8分
∴

∴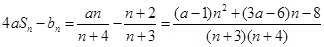
由条件可知 恒成立即可满足条件
恒成立即可满足条件
解:(1)
∵ ∴
∴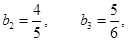 ……………3分
……………3分
(2)∵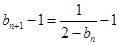 ∴
∴
∴数列{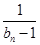 }是以-4为首项,-1为公差的等差数列。 ……………5分
}是以-4为首项,-1为公差的等差数列。 ……………5分
∴ ∴
∴ ……………7分
……………7分
(3) ……………8分
……………8分
∴
 ……………9分
……………9分
∴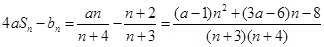 ……………10分
……………10分
由条件可知 恒成立即可满足条件
恒成立即可满足条件
设 ……………11分
……………11分
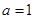 时,
时, 恒成立, ∴
恒成立, ∴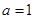 可取;
可取;
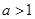 时,由二次函数的性质知不可能成立;∴
时,由二次函数的性质知不可能成立;∴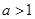 不可取;
不可取;
 时,对称轴
时,对称轴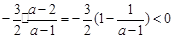
 在
在 为单调递减函数. 故只要
为单调递减函数. 故只要 即可,
即可,
由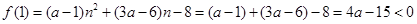
得 ∴
∴ 时
时 恒成立 ……………13分
恒成立 ……………13分
综上知:实数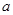 的取值范围为
的取值范围为 . ……………14分
. ……………14分
 ,递推关系得到,
,递推关系得到,∵
 ∴
∴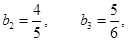
第二问中,∵
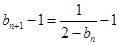 ∴
∴
∴数列{
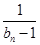 }是以-4为首项,-1为公差的等差数列。∴
}是以-4为首项,-1为公差的等差数列。∴
第三问中,
 ……………8分
……………8分 ∴


∴
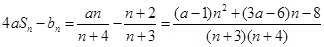
由条件可知
 恒成立即可满足条件
恒成立即可满足条件解:(1)

∵
 ∴
∴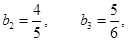 ……………3分
……………3分(2)∵
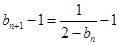 ∴
∴
∴数列{
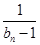 }是以-4为首项,-1为公差的等差数列。 ……………5分
}是以-4为首项,-1为公差的等差数列。 ……………5分∴
 ∴
∴ ……………7分
……………7分(3)
 ……………8分
……………8分∴

 ……………9分
……………9分∴
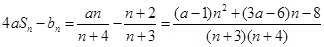 ……………10分
……………10分由条件可知
 恒成立即可满足条件
恒成立即可满足条件设
 ……………11分
……………11分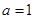 时,
时, 恒成立, ∴
恒成立, ∴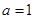 可取;
可取;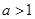 时,由二次函数的性质知不可能成立;∴
时,由二次函数的性质知不可能成立;∴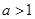 不可取;
不可取; 时,对称轴
时,对称轴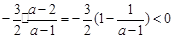
 在
在 为单调递减函数. 故只要
为单调递减函数. 故只要 即可,
即可,由
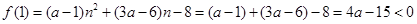
得
 ∴
∴ 时
时 恒成立 ……………13分
恒成立 ……………13分综上知:实数
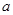 的取值范围为
的取值范围为 . ……………14分
. ……………14分
练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
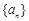 和
和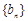 满足:
满足: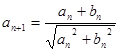 ,
,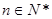 ,
,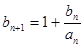 ,
,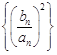 是等差数列;
是等差数列;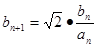 ,
,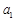 和
和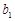 的值.
的值.
 ,
,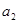 ,-1四个实数成等差数列,-4,
,-1四个实数成等差数列,-4,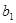 ,
,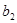 ,
,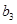 ,-1五个实数成
,-1五个实数成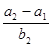 =
= 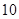 项的和为
项的和为 项的和为
项的和为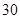 ,则前
,则前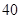 项的和为 ▲ .
项的和为 ▲ .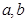 ,可按规则
,可按规则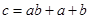 扩充为一个新数
扩充为一个新数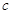 ,在
,在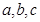 三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.若
三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.若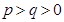 ,经过6次操作后扩充所得的数为
,经过6次操作后扩充所得的数为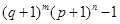 (
(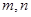 为正整数),则
为正整数),则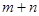 的值为 ▲ .
的值为 ▲ .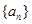 是首项为0的递增数列,
是首项为0的递增数列,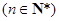 ,
,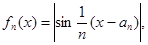
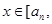
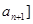 满足:对于任意的
满足:对于任意的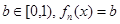 总有两个不同的根. (Ⅰ)试写出
总有两个不同的根. (Ⅰ)试写出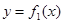 ,并求出
,并求出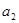 ;
; 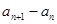 ,并求出
,并求出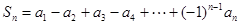 ,求
,求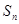 .
.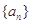 满足:所有的奇数项
满足:所有的奇数项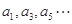 构成以1为首项,1为公差的等差数列;所有的偶数项
构成以1为首项,1为公差的等差数列;所有的偶数项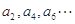 构成以2为首项,3为公差的等差数列,则
构成以2为首项,3为公差的等差数列,则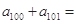 ( )
( )
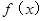 =
=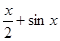 的所有正的极小值点从小到大排成的数列为
的所有正的极小值点从小到大排成的数列为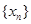 .
.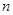 项和为
项和为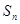 ,求
,求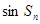 .
.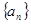 中,
中,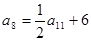 ,则数列
,则数列 项和
项和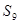 等于( )
等于( )


