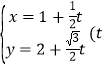题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且经过点
,且经过点![]() ,一条直线
,一条直线![]() 与椭圆C交于
与椭圆C交于![]() ,
,![]() 两点,以
两点,以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() .
.
(1)求椭圆C的标准方程;
(2)求证:![]() 为定值.
为定值.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)因为椭圆经过点![]() ,所以
,所以![]() ,再根据离心率,即可求得椭圆的方程;
,再根据离心率,即可求得椭圆的方程;
(2)①若直线![]() 的斜率存在时,
的斜率存在时,![]() ,
,![]() ,
,![]() ,与椭圆方程联立,由
,与椭圆方程联立,由![]() 可得
可得![]() ,从而得到
,从而得到![]() 的关系,结合点到直线的距离公式,可证明结论;②若直线
的关系,结合点到直线的距离公式,可证明结论;②若直线![]() 的斜率不存在,则有
的斜率不存在,则有![]() ,可证结论也成立.
,可证结论也成立.
(1)因为椭圆经过点![]() ,所以
,所以![]() ,
,
又因为![]() ,则
,则![]() ,由
,由![]() ,得
,得![]() ,
,
所以椭圆的标准方程为![]() .
.
(2)①若直线![]() 的斜率存在时,设
的斜率存在时,设![]() ,与椭圆方程联立得:
,与椭圆方程联立得:
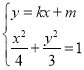 ,有
,有![]() ,
,
由题意,![]() ,设
,设![]() ,
,![]() ,
,
![]() ,
,![]() .
.
因为以![]() 为直径的圆过原点
为直径的圆过原点![]() ,
,
由![]() ,得
,得 ![]() ,
,
即![]() ,整理得,
,整理得,
![]() ,
,
而![]()
设h为![]() 到
到![]() 的距离,则
的距离,则
![]()
所以![]() ,
,
而![]() ,
,
所以![]()
![]() .
.
②若直线![]() 的斜率不存在,则有
的斜率不存在,则有![]() ,
,
不妨设![]() ,设
,设![]() ,有
,有![]() ,
,
代入椭圆方程![]() 得,
得,![]() ,
,
![]() ,
,
即![]() ,
,
综上![]() .
.

练习册系列答案
相关题目
【题目】金秋九月,丹桂飘香,某高校迎来了一大批优秀的学生.新生接待其实也是和社会沟通的一个平台.校团委、学生会从在校学生中随机抽取了160名学生,对是否愿意投入到新生接待工作进行了问卷调查,统计数据如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女士 | 40 | 40 |
(1)根据上表说明,能否有99%把握认为愿意参加新生接待工作与性别有关;
(2)现从参与问卷调查且愿意参加新生接待工作的学生中,采用按性别分层抽样的方法,选取10人.若从这10人中随机选取3人到火车站迎接新生,设选取的3人中女生人数为![]() ,写出
,写出![]() 的分布列,并求
的分布列,并求![]() .
.
附: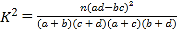 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |