题目内容
【题目】求经过点![]() 且分别满足下列条件的直线的一般式方程.
且分别满足下列条件的直线的一般式方程.
(1)倾斜角为45°;
(2)在![]() 轴上的截距为5;
轴上的截距为5;
(3)在第二象限与坐标轴围成的三角形面积为4.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)利用斜率和倾斜角的关系,可以求出斜率,可以用点斜式写出直线方程,最后化为一般方程;
(2)设出直线的斜截式方程,把点代入方程中求出斜率,进而可求出方程,化为一般式方程即可;
(3)设出直线的截距式方程,利用面积公式和已知条件,可以求出所设参数,即可求出直线方程,化为一般式即可.
(1)因为直线的倾斜角为45°,所以斜率![]() ,
,
代入点斜式![]() ,即
,即![]() .
.
(2)因为直线在![]() 轴上的截距是5,所以设直线方程为:
轴上的截距是5,所以设直线方程为:![]() ,
,
代入点![]() 得
得![]() ,故直线方程为
,故直线方程为![]() .
.
(3)设所求直线方程为![]()
则![]() ,
,![]() 即
即![]() ,
,
解之得![]() ,
,![]() ,
,
所以直线方程为![]() ,即
,即![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】现在很多人喜欢自助游,2017年孝感杨店桃花节,美丽的桃花风景和人文景观迎来众多宾客.某调查机构为了了解“自助游”是否与性别有关,在孝感桃花节期间,随机抽取了![]() 人,得如下所示的列联表:
人,得如下所示的列联表:
赞成“自助游” | 不赞成“自助游” | 合计 | |
男性 |
| ||
女性 |
| ||
合计 |
|
(1)若在![]() 这人中,按性别分层抽取一个容量为
这人中,按性别分层抽取一个容量为![]() 的样本,女性应抽
的样本,女性应抽![]() 人,请将上面的列联表补充完整,并据此资料能否在犯错误的概率不超过
人,请将上面的列联表补充完整,并据此资料能否在犯错误的概率不超过![]() 前提下,认为赞成“自助游”是与性别有关系?
前提下,认为赞成“自助游”是与性别有关系?
(2)若以抽取样本的频率为概率,从旅游节大量游客中随机抽取![]() 人赠送精美纪念品,记这
人赠送精美纪念品,记这![]() 人中赞成“自助游”人数为
人中赞成“自助游”人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附: 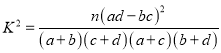
|
|
|
|
|
|
|
|
|
|