题目内容
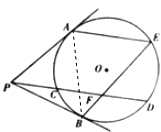
【题目】如图所示,过点P分别做圆O的切线PA、PB和割线PCD,弦BE交CD于F,满足P、B、F、A四点共圆.
(Ⅰ)证明:AE∥CD;
(Ⅱ)若圆O的半径为5,且PC=CF=FD=3,求四边形PBFA的外接圆的半径.
【答案】( I)证明:连接AB.
∵P、B、F、A四点共圆,∴∠PAB=∠PFB.
又PA与圆O切于点A,∴∠PAB=∠AEB,
∴∠PFB=∠AEB∴AE∥CD.
( II)解:因为PA、PB是圆O的切线,所以P、B、O、A四点共圆,
由△PAB外接圆的唯一性可得P、B、F、A、O共圆,
四边形PBFA的外接圆就是四边形PBOA的外接圆,∴OP是该外接圆的直径.
由切割线定理可得PA2=PCPD=3×9=27
∴ ![]() .
.
∴四边形PBFA的外接圆的半径为 ![]() .
.
【解析】(Ⅰ)连接AB,利用P、B、F、A四点共圆,PA与圆O切于点A,得出两组角相等,即可证明:AE∥CD;(Ⅱ)四边形PBFA的外接圆就是四边形PBOA的外接圆,OP是该外接圆的直径,由切割线定理可得PA,即可求四边形PBFA的外接圆的半径.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
【题目】![]() 市某机构为了调查该市市民对我国申办2034年足球世界杯的态度,随机选取了
市某机构为了调查该市市民对我国申办2034年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
不支持 | 支持 | 合计 | |
男性市民 |
| ||
女性市民 |
| ||
合计 |
|
|
(1)根据已知数据把表格数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
(i)能否有![]() 的把握认为支持申办足球世界杯与性别有关;
的把握认为支持申办足球世界杯与性别有关;
(ii)已知在被调查的支持申办足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教师,现从这
位是教师,现从这![]() 位退体老人中随机抽取
位退体老人中随机抽取![]() 人,求至多有
人,求至多有![]() 位老师的概率.
位老师的概率.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|





