题目内容
(2013•湖南模拟)已知f(x)=ax+
+3-2a(a,b∈R)的图象在点(1,f(1)处的切线与直线y=3x+1平行.
(1)求a与b满足的关系式;
(2)若a>0且f(x)≥3lnx在[1,+∞)上恒成立,求a的取值范围.
| b | x |
(1)求a与b满足的关系式;
(2)若a>0且f(x)≥3lnx在[1,+∞)上恒成立,求a的取值范围.
分析:(1)根据f(x)在点(1,f(1)处的切线与直线y=3x+1平行建立等式关系:f'(1)=3,即可求出a与b的关系式;
(2)先构造函数g(x)=f(x)-3lnx=ax+
+3-2a-3lnx,x∈[1,+∞),利用导数研究g(x)的最小值,讨论a的范围,分别进行求解即可求出a的取值范围.
(2)先构造函数g(x)=f(x)-3lnx=ax+
| a-3 |
| x |
解答:解:(1)f′(x)=a-
,
由于f(x)=ax+
+3-2a(a,b∈R)的图象在点(1,f(1)处的切线与直线y=3x+1平行,
则有f′(1)=a-b=3,即b=a-3,
此时,f(1)=a+a-3+3-2a=0≠4,
(2)由f(x)≥3lnx在[1,+∞)上恒成立,得
ax+
+3-2a-3lnx≥0在[1,+∞)上恒成立,
令g(x)=ax+
+3-2a-3lnx,x∈[1,+∞)
则g(l)=0,g′(x)=a-
-
=
.
(i)当a>
,
≤l
则g′(x)>0,g(x)在[1,+∞)上是增函数,
所以g(x)≥g(l)=0,f(x)>3lnx,故f(x)≥3lnx在[1,+∞)上恒成立.
(ii)a=
时,g′(x)≥0,g(x)在[1,+∞)上是增函数,
所以g(x)≥g(l)=0,f(x)>3lnx,故f(x)≥3lnx在[1,+∞)上恒成立.
(iii)当0<a<
,
>l,
则x∈(1,
)时,g′(x)<0,g(x)在[1,+∞)上是减函数,
x∈(
,+∞)时,g′(x)>0,g(x)在[1,+∞)上是增函数,
所以存在x0∈(1,
),使得g(x0)<g(l)=0,即存在x0∈(1,
),使得f(x0)>3lnx0不成立,
综上所述,所求a的取值范围为[
,+∞).
| b |
| x2 |
由于f(x)=ax+
| b |
| x |
则有f′(1)=a-b=3,即b=a-3,
此时,f(1)=a+a-3+3-2a=0≠4,
(2)由f(x)≥3lnx在[1,+∞)上恒成立,得
ax+
| a-3 |
| x |
令g(x)=ax+
| a-3 |
| x |
则g(l)=0,g′(x)=a-
| a-3 |
| x2 |
| 3 |
| x |
a(x-
| ||
| x2 |
(i)当a>
| 3 |
| 2 |
| 3-a |
| a |
则g′(x)>0,g(x)在[1,+∞)上是增函数,
所以g(x)≥g(l)=0,f(x)>3lnx,故f(x)≥3lnx在[1,+∞)上恒成立.
(ii)a=
| 3 |
| 2 |
所以g(x)≥g(l)=0,f(x)>3lnx,故f(x)≥3lnx在[1,+∞)上恒成立.
(iii)当0<a<
| 3 |
| 2 |
| 3-a |
| a |
则x∈(1,
| 3-a |
| a |
x∈(
| 3-a |
| a |
所以存在x0∈(1,
| 3-a |
| a |
| 3-a |
| a |
综上所述,所求a的取值范围为[
| 3 |
| 2 |
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及函数恒成立问题等基础题知识,考查运算求解能力,考查化归与转化思想,分类讨论思想,属于中档题.

练习册系列答案
相关题目
 (2013•湖南模拟)设椭圆
(2013•湖南模拟)设椭圆 (2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=
(2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=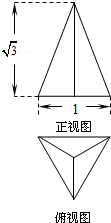 (2013•湖南模拟)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )
(2013•湖南模拟)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( ) (2013•湖南模拟)已知集合M={x∈Z|-1≤x≤1},N={x∈Z|x(x-2)≤0},则如图所示韦恩图中的阴影部分所表示的集合为( )
(2013•湖南模拟)已知集合M={x∈Z|-1≤x≤1},N={x∈Z|x(x-2)≤0},则如图所示韦恩图中的阴影部分所表示的集合为( )