题目内容
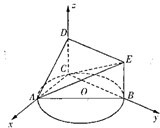
 (2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=
(2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=
| ||
| 2 |
(1)证明:平面ACD⊥平面ADE,
(2)令AC=x,V(x) 表示三棱锥A-CBE的体积,当V(x) 取得最大值时,求直线AD与平面ACE所成角的正弦值.
分析:(1)欲证平面ACD⊥平面ADE,根据面面垂直的判定定理可知在平面ADE内一直线与平面ACD垂直,而根据BC⊥平面ADC,DE∥BC,可得DE⊥平面ADC;
(2)先利用等体积法表示出三棱锥A-CBE的体积,利用基本不等式求最值,再建立空间直角坐标系,利用向量的夹角公式,即可求得直线AD与平面ACE所成角的正弦值.
(2)先利用等体积法表示出三棱锥A-CBE的体积,利用基本不等式求最值,再建立空间直角坐标系,利用向量的夹角公式,即可求得直线AD与平面ACE所成角的正弦值.
解答:(1)证明:∵四边形DCBE为平行四边形,∴CD∥BE,BC∥DE
∵DC⊥平面ABC,BC?平面ABC,∴DC⊥BC
∵AB是圆O的直径,∴BC⊥AC
∵DC∩AC=C,∴BC⊥平面ADC.
∵DE∥BC,
∴DE⊥平面ADC
又∵DE?平面ADE,∴平面ACD⊥平面ADE;
(2)∵DC⊥平面ABC,CD∥BE,∴BE⊥平面ABC
∵AB?平面ABC,∴BE⊥AB,
在Rt△ABE中,由tan∠EAB=
=
,AB=2得BE=
在Rt△ABC中,∵BC=
=
(0<x<2)
∴S△ABC=
AC•BC=
x
∴V(x)=VC-ABE=VE-ABC=
S△ABC•BE=
x
=
(0<x<2)
∵0<x<2,∴
≤
=2
∴V(x)≤
,当且仅当x2=4-x2,即x=
时,V(x)取得最大值,AC=
这时△ABC为等腰直角三角形
建立如图所示的坐标系,
C(0,0,0),A(
,0,0),E(0,
,
),D(0,0,
),
=(-
,0,
)
设平面AEC的法向量
=(x,y,z),则
,∴
,∴可取
=(0,-
,
)
设直线AD与平面ACE所成角为θ,则sinθ=cos<
,
>=
=
=
故直线AD与平面ACE所成角的正弦值为
∵DC⊥平面ABC,BC?平面ABC,∴DC⊥BC
∵AB是圆O的直径,∴BC⊥AC
∵DC∩AC=C,∴BC⊥平面ADC.
∵DE∥BC,
∴DE⊥平面ADC
又∵DE?平面ADE,∴平面ACD⊥平面ADE;
(2)∵DC⊥平面ABC,CD∥BE,∴BE⊥平面ABC
∵AB?平面ABC,∴BE⊥AB,
在Rt△ABE中,由tan∠EAB=
| BE |
| AB |
| ||
| 2 |
| 3 |
在Rt△ABC中,∵BC=
| AB2-AC2 |
| 4-x2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 4-x2 |
∴V(x)=VC-ABE=VE-ABC=
| 1 |
| 3 |
| ||
| 6 |
| 4-x2 |
| ||
| 6 |
| x2(4-x2) |
∵0<x<2,∴
| x2(4-x2) |
| x2+4-x2 |
| 2 |
∴V(x)≤
| ||
| 3 |
| 2 |
| 2 |
这时△ABC为等腰直角三角形
建立如图所示的坐标系,

C(0,0,0),A(
| 2 |
| 2 |
| 3 |
| 3 |
| AD |
| 2 |
| 3 |
设平面AEC的法向量
| n |
|
|
| n |
| 3 |
| 2 |
设直线AD与平面ACE所成角为θ,则sinθ=cos<
| AD |
| n |
|
| ||||
|
|
| ||||
|
| ||
| 5 |
故直线AD与平面ACE所成角的正弦值为
| ||
| 5 |
点评:本题主要考查空间中的线面关系,考查面面垂直的判定及简单组合体体积的计算,考查线面角,考查向量知识的运用,属于中档题.

练习册系列答案
相关题目
 (2013•湖南模拟)设椭圆
(2013•湖南模拟)设椭圆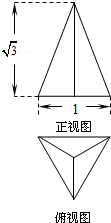 (2013•湖南模拟)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )
(2013•湖南模拟)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( ) (2013•湖南模拟)已知集合M={x∈Z|-1≤x≤1},N={x∈Z|x(x-2)≤0},则如图所示韦恩图中的阴影部分所表示的集合为( )
(2013•湖南模拟)已知集合M={x∈Z|-1≤x≤1},N={x∈Z|x(x-2)≤0},则如图所示韦恩图中的阴影部分所表示的集合为( )