题目内容
 (2013•湖南模拟)设椭圆C:
(2013•湖南模拟)设椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| BF2 |
| BF1 |
(1)若过A、B、F2三点的圆恰好与直线x-
| 3 |
(2)在(1)的条件下,过右焦点F2作斜率为k的直线l与椭圆C交于M、N两点,在x轴上是否存在点P(m,0),使得以PM,PN为邻边的平行四边形是菱形,如果存在,求出m的取值范围;如果不存在,说明理由.
分析:(1)根据
=
,得c=
a,所以|F1F2|=a,利用
=2
,可得F1为BF2的中点,从而可得△ABF2的外接圆圆心为F1(-
,0),半径r=|F1A|=a,根据过A、B、F2三点的圆与直线x-
y-3=0相切,利用点到直线的距离公式,即可确定椭圆方程;
(2)由(1)知F2(1,0),设l的方程为:y=k(x-1)与椭圆方程联立,利用韦达定理,结合菱形对角线垂直,所以(
+
)•
=0,可得m,k之间的关系,从而可得结论.
| c |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| BF2 |
| BF1 |
| a |
| 2 |
| 3 |
(2)由(1)知F2(1,0),设l的方程为:y=k(x-1)与椭圆方程联立,利用韦达定理,结合菱形对角线垂直,所以(
| PM |
| PN |
| MN |
解答:解:(1)由题意
=
,得c=
a,所以|F1F2|=a
∵|AF1|=|AF2|=a,
=2
,∴F1为BF2的中点,
∴|AF1|=|AF2|=|F1F2|=a
∴△ABF2的外接圆圆心为F1(-
,0),半径r=|F1A|=a…(3分)
又过A、B、F2三点的圆与直线x-
y-3=0相切,所以
=a
∴a=2,∴c=1,b2=a2-c2=3.
∴所求椭圆方程为
+
=1…(6分)
(2)由(1)知F2(1,0),设l的方程为:y=k(x-1)
将直线方程与椭圆方程联立
,整理得(3+4k2)x2-8k2x+4k2-12=0
设M(x1,y1),N(x2,y2),则x1+x2=
, y1+y2=k(x1+x2-2)…(8分)
假设存在点P(m,0),使得以PM,PN为邻边的平行四边形是菱形,
由于菱形对角线垂直,所以(
+
)•
=0
又
+
=(x1-m,y1)+(x2-m,y2)=(x1+x2-2m, y1+y2)
又MN的方向向量是(1,k),故k(y1+y2)+x1+x2-2m=0,则k2(x1+x2-2)+x1+x2-2m=0,
即k2(
-2)+
-2m=0
由已知条件知k≠0且k∈R,
∴m=
=
…(11分)
∴0<m<
,
故存在满足题意的点P且m的取值范围是(0,
)…(13分)
| c |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
∵|AF1|=|AF2|=a,
| BF2 |
| BF1 |
∴|AF1|=|AF2|=|F1F2|=a
∴△ABF2的外接圆圆心为F1(-
| a |
| 2 |
又过A、B、F2三点的圆与直线x-
| 3 |
|-
| ||
| 2 |
∴a=2,∴c=1,b2=a2-c2=3.
∴所求椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)由(1)知F2(1,0),设l的方程为:y=k(x-1)
将直线方程与椭圆方程联立
|
设M(x1,y1),N(x2,y2),则x1+x2=
| 8k2 |
| 3+4k2 |
假设存在点P(m,0),使得以PM,PN为邻边的平行四边形是菱形,
由于菱形对角线垂直,所以(
| PM |
| PN |
| MN |
又
| PM |
| PN |
又MN的方向向量是(1,k),故k(y1+y2)+x1+x2-2m=0,则k2(x1+x2-2)+x1+x2-2m=0,
即k2(
| 8k2 |
| 3+4k2 |
| 8k2 |
| 3+4k2 |
由已知条件知k≠0且k∈R,
∴m=
| k2 |
| 3+4k2 |
| 1 | ||
|
∴0<m<
| 1 |
| 4 |
故存在满足题意的点P且m的取值范围是(0,
| 1 |
| 4 |
点评:本题考查椭圆的标准方程,考查直线与圆,直线与椭圆的位置关系,考查韦达定理的运用,确定椭圆方程,正确运用韦达定理是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=
(2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=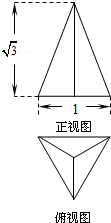 (2013•湖南模拟)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )
(2013•湖南模拟)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( ) (2013•湖南模拟)已知集合M={x∈Z|-1≤x≤1},N={x∈Z|x(x-2)≤0},则如图所示韦恩图中的阴影部分所表示的集合为( )
(2013•湖南模拟)已知集合M={x∈Z|-1≤x≤1},N={x∈Z|x(x-2)≤0},则如图所示韦恩图中的阴影部分所表示的集合为( )