题目内容

16．在等比数列{an}中，有a3a11=4a7，数列{bn}是等差数列，且b7=a7，则b5+b9=8．

分析 由a3a11=4a7，解出a7的值，由 b5+b9=2b7 =2a7 求得结果．

解答 解：等比数列{an}中，由a3a11=4a7，可知a72=4a7，∴a7=4，
∵数列{bn}是等差数列，∴b5+b9=2b7 =2a7 =8，
故答案为：8．

点评 本题考查等差数列、等比数列的性质，求出a7的值是解题的关键，是基础题．

练习册系列答案
相关题目
6．已知集合P={x∈Z||x-1|＜2}，Q={x∈Z|-1≤x≤2}，则P∩Q=（　　）
A．{0，1，2}B．{-1，0，1}C．{-1，0，1，2}D．{1，2}
7．已知△ABC是正三角形，若$\overrightarrow{a}$=$\overrightarrow{AC}$-$λ\overrightarrow{AB}$与向量$\overrightarrow{AC}$的夹角大于90°，则实数λ的取值范围是（　　）
A．（2，+∞）B．（-∞，-2）C．（-∞，-1）D．（1，+∞）
4．△ABC的三边成等差数列，最大边长为26，且它所对角的余弦值为$\frac{1}{6}$，则最小边长为（　　）
A．18B．24C．12D．16
11．在△ABC中，a，b，c分别是角A，B，C所对的边，O为△ABC三边中垂线的交点．
（1）若b-c=$\frac{1}{4}$a，2sinB=3sinC，求cosA的值；
（2）若b2-2b+c2=0，求$\overrightarrow{BC}$•$\overrightarrow{AO}$的取值范围．
1．已知数列{an}的前n项和为Sn，满足Sn=2（an-n），n∈N+*．
（1）证明：{an+2}是等比数列，并求{an}的通项公式；
（2）若数列{bn}满足bn=log2（an+2），Tn为数列{$\frac{1}{{b}_{n}{b}_{n+1}}$}的前n项和，求Tn．
8．已知函数f（x）=x2-2ax+5（a＞1），若f（x）在区间（-∞，2]上是减函数，且对任意的x1，x2∈[1，a+1]，总有|f（x1）-f（x2）|≤4，求a的取值范围．
5．M科技公司从45名男员工、30名女员工中按照分层抽样的方法组建了一个5人的科研小组．
（1）求某员工被抽到的概率及科研小组中男女员工的人数；
（2）这个科研小组决定选出两名员工做某项实验，方法是先从小组中选出1名员工做实验，该员工做完后，再从小组内剩下的员工中选一名员工做实验，求选出的两名员工中恰有一名女员工的概率．
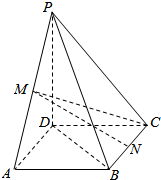6．如图，在四棱锥P-ABCD中，底面ABCD是正方形，PD⊥底面ABCD，M，N分别为PA，BC的中点，且PD=AD=$\sqrt{2}$
（1）求证：MN∥平面PCD；
（2）求证：平面PAC⊥平面PBD．
（3）求三棱锥A-MBC的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网