题目内容
设命题P:关于x的不等2x<a的解集为∅;命题q:函数y=lg(ax2-x+a)的定义域是R.若“p∨q”为真,“p∧q”为假,求a的取值范围.
因为2x>0,所以要使关于x的不等2x<a的解集为∅,则a≤0,即p真:a≤0;则p假:a>0.
要使函数y=lg(ax2-x+a)的定义域是R,则
,解得a>
,即q真:a>
;则q假:a≤
.
若“p∨q”为真,“p∧q”为假,则p真q假或p假q真.
若p真q假,则a≤0;若p假q真,则a>
.
故“p∨q”为真,“p∧q”为假的a的取值范围是(-∞,0]∪(
,+∞).
要使函数y=lg(ax2-x+a)的定义域是R,则
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
若“p∨q”为真,“p∧q”为假,则p真q假或p假q真.
若p真q假,则a≤0;若p假q真,则a>
| 1 |
| 2 |
故“p∨q”为真,“p∧q”为假的a的取值范围是(-∞,0]∪(
| 1 |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
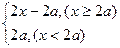 ,函数y>1恒成立, 若p∧q为假,p∨q为真,求a的取值范围
,函数y>1恒成立, 若p∧q为假,p∨q为真,求a的取值范围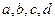 是实数,若
是实数,若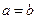 ,
,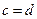 ,则
,则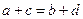 ”,对其原命题、逆命题、否命题呼逆否命题而言,真命题有( )
”,对其原命题、逆命题、否命题呼逆否命题而言,真命题有( ) 定义双阶乘
定义双阶乘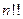 如下:当
如下:当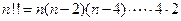 ;当
;当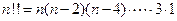 ,现有如下四个命题:①
,现有如下四个命题:①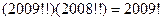 ;
;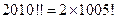 ;
; ③设
③设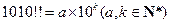 ,若
,若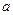 的个位数不是0,则
的个位数不是0,则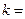 112;
112;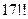
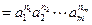 (
(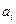 为正质数,
为正质数,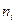 为正整数
为正整数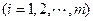 ),则
),则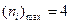 ;
; 的周期为
的周期为 ②已知数列
②已知数列 的前n项和为Sn,若a1=1且an+1=Sn+1,则数列
的前n项和为Sn,若a1=1且an+1=Sn+1,则数列 的图象关于点(-1,1)对称;④已知命题
的图象关于点(-1,1)对称;④已知命题 :对任意的
:对任意的 ,都有
,都有 ,则
,则 :存在
:存在 。其中所有真命题的序号是 。
。其中所有真命题的序号是 。