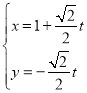Question

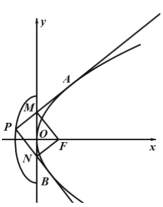
【题目】如图，设抛物线的焦点为F，点P是半椭圆上的一点，过点P作抛物线C的两条切线，切点分别为A、B，且直线PA、PB分别交y轴于点M、N．

（1）证明：；

（2）求的取值范围．

Answer 1

【答案】（1）证明见解析 （2）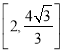

【解析】

（1）设点P的坐标为，由直线PA与椭圆相切，得，要证明，只需证明，即证即可；

（2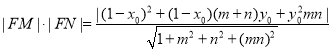），，，由（1）易得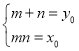，代入化简即可.

（1）由题意知，直线PA的斜率存在且不为0，设点P的坐标为，

直线PA方程为．

令，可知点M的坐标为．

由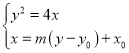，消去x得．

因为直线与抛物线只有一个交点，

故，即．

因为点F的坐标为，

故，．

则．

因此，亦即．

（2）设直线PB的方程为．

由（1）可知，n满足方程．

故m，n是关于t的方程的两个不同的实根．

所以．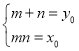

由（1）可知：，同理可得．

故，．

则，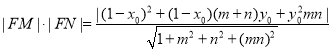

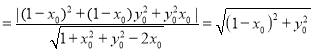
因为，

所以．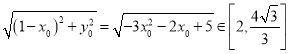

因此，的取值范围是．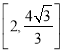

【点晴】

本题考查直线与椭圆的位置关系，计算量较大，考查学生的运算求解能力、转化与化归的思想，是一道中档题.