题目内容
9.已知圆C:x2+y2=4,动抛物线过A(-1,0),B(1,0)两点,且以圆的切线为准线,则抛物线焦点的轨迹方程为$\frac{{x}^{2}}{4}$$+\frac{{y}^{2}}{3}$=1(y≠0).分析 可设焦点为P,根据抛物线的定义便有|PA|+||PB|=d1+d2,d1,d2分别表示点A,B到切线的距离,而能够知道该距离等于原点O到切线距离的2倍,从而得出|PA|+|PB|=4,这样便可得出抛物线的焦点轨迹为椭圆.
解答  解:画出抛物线的大致图象如下:
解:画出抛物线的大致图象如下:
根据抛物线的定义知:A,B两点到焦点P的距离和等于A,B两点到准线距离的和;
而A,B两点到准线的距离和等于O到准线距离和的2倍;
∴|PA|+|PB|=4;
∴焦点的轨迹是以A,B为焦点的椭圆,∴a=2,c=1;
∴焦点的轨迹方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$(y≠0).
故答案为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1,(y≠0)$.
点评 考查抛物线的定义,梯形中位线的性质,抛物线的焦点和准线的概念,以及椭圆的定义.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
1.实数x,y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{2x-y-5≤0}\end{array}\right.$,则z=x+2y-4的最大值为( )
| A. | 18 | B. | 19 | C. | 20 | D. | 21 |
18.若a、b为任意非零实数,且a>b,则下列不等式成立的是( )
| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | $\frac{b}{a}<1$ | C. | lg(a-b)>0 | D. | ${(\frac{1}{3})^a}<{(\frac{1}{3})^b}$ |
19.复数z=a2+b2+(a+|a|)i(a、b∈R)为实数的充要条件是( )
| A. | |a|=|b| | B. | a<0且a=-b | C. | a>0且a≠b | D. | a≤0 |
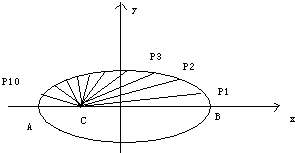 极坐标方程ρ=$\frac{ep}{1-ecosθ}$,(p>0,e>0),可以转化为平面直角坐标方程$\frac{{\sqrt{{x^2}+{y^2}}}}{{|{x+p}|}}$=e,该式子可以解释为:点(x,y)到原点的距离与到x=-p的距离之比为e,根据圆锥曲线的定义可以得到:ρ=$\frac{ep}{1-ecosθ}$表示一个以原点为其中一个焦点,以x=-p为对应准线的圆锥曲线.如图:过椭圆$\frac{x^2}{16}$+$\frac{y^2}{9}$=1的左焦点C作CP1,CP2,CP3…CP10等分∠ACB(A,B分别为椭圆的左右顶点),记P1,P2,P3…P10到左准线的距离分别为d1,d2,d3…d10,则$\frac{1}{d_1}$+$\frac{1}{d_2}$+$\frac{1}{d_3}$+…+$\frac{1}{{{d_{10}}}}$=$\frac{{10\sqrt{7}}}{9}$.
极坐标方程ρ=$\frac{ep}{1-ecosθ}$,(p>0,e>0),可以转化为平面直角坐标方程$\frac{{\sqrt{{x^2}+{y^2}}}}{{|{x+p}|}}$=e,该式子可以解释为:点(x,y)到原点的距离与到x=-p的距离之比为e,根据圆锥曲线的定义可以得到:ρ=$\frac{ep}{1-ecosθ}$表示一个以原点为其中一个焦点,以x=-p为对应准线的圆锥曲线.如图:过椭圆$\frac{x^2}{16}$+$\frac{y^2}{9}$=1的左焦点C作CP1,CP2,CP3…CP10等分∠ACB(A,B分别为椭圆的左右顶点),记P1,P2,P3…P10到左准线的距离分别为d1,d2,d3…d10,则$\frac{1}{d_1}$+$\frac{1}{d_2}$+$\frac{1}{d_3}$+…+$\frac{1}{{{d_{10}}}}$=$\frac{{10\sqrt{7}}}{9}$.