已知定点A(1.0)和定直线l:x=-1.在l上有两动点E.F且满足AE⊥AF.另有动点P.满足EP∥OA.FO∥OP.且动点P的轨迹方程为( ) A.y2=4xB.y2=4xC.y2=-4xD.y2=-4x 题目和参考答案——青夏教育精英家教网—

题目内容

已知定点A（1，0）和定直线l：x=-1，在l上有两动点E，F且满足

⊥

，另有动点P，满足

∥

，

∥

（O为坐标原点），且动点P的轨迹方程为（　　）

A、y²=4x

B、y²=4x（x≠0）

C、y²=-4x

D、y²=-4x（x≠0）

分析：设P（x，y），欲动点P的轨迹方程，即寻找x，y之间的关系式，利用向量间的关系求出向量

、

的坐标后垂直条件即得动点P的轨迹方程．

解答：解：设P（x，y），E（-1，y₁），F（-1，y₂）（y₁，y₂均不为零）
由

∥

?y₁=y，即E（-1，y）．
由

∥

?y2=-

．
由

⊥

?y²=4x（x≠0）．
故选B．

点评：本题主要考查了轨迹方程的问题．本题解题的关键是利用了向量平行和垂直的坐标运算求得轨迹方程．

练习册系列答案

相关题目

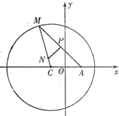如图，已知定点A（1，0），定圆C：（x+1）²+y²=8，M为圆C上的一个动点，点P在线段AM上，点N在线段CM上，且满足

．

，且f（1）=1，f（-2）=4．
（1）求a、b的值；
（2）已知定点A（1，0），设点P（x，y）是函数y=f（x）（x＜-1）图象上的任意一点，求|AP|的最小值，并求此时点P的坐标；
（3）当x∈[1，2]时，不等式f(x)≤

(x+1)|x-m|

恒成立，求实数m的取值范围．

已知定点A（1，0）和定直线x=-1上的两个动点E、F，满足

（其中O为坐标原点）．
（1）求动点P的轨迹C的方程；
（2）过点B（0，2）的直线l与（1）中轨迹C相交于两个不同的点M、N，若

•

＜0，求直线l的斜率的取值范围．

已知定点A（1，0），定直线l：x=5，动点M（x，y）
（Ⅰ）若M到点A的距离与M到直线l的距离之比为

，试求M的轨迹曲线C₁的方程．
（Ⅱ）若曲线C₂是以C₁的焦点为顶点，且以C₁的顶点为焦点，试求曲线C₂的方程．

已知定点A（1，0）和定圆B：x²+y²+2x-15=0，动圆P和定圆B相切并过A点，
（1）求动圆P的圆心P的轨迹C的方程．
（2）设Q是轨迹C上任意一点，求∠AQB的最大值．

试题分类