题目内容
已知A是曲线ρ=3cosθ上任意一点,求点A到直线ρcosθ=1距离的最大值和最小值。
最大值为2,最小值为0
将极坐标方程转化成直角坐标方程:
ρ=3cosθ即:x2+y2=3x,(x-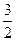 )2+y2=
)2+y2=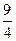 3′
3′
ρcosθ=1即x="1 " 6′
直线与圆相交。
所求最大值为2, 8′
最小值为0。 10′
ρ=3cosθ即:x2+y2=3x,(x-
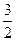 )2+y2=
)2+y2=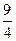 3′
3′ρcosθ=1即x="1 " 6′
直线与圆相交。
所求最大值为2, 8′
最小值为0。 10′

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目

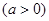
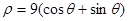
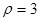
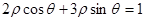
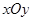 中,点P的直角坐标为
中,点P的直角坐标为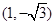 。若以圆点O为极点,
。若以圆点O为极点,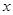 轴半轴为极轴建立坐标系,则点P的极坐标可以是
轴半轴为极轴建立坐标系,则点P的极坐标可以是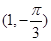

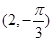
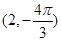
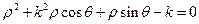 关于直线l:
关于直线l: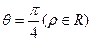 对称的充要条件是 ()
对称的充要条件是 () 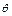 =
=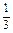 化为直角坐标方程,并说明该方程表示什么曲线.
化为直角坐标方程,并说明该方程表示什么曲线.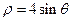 相切的一条直线的方程为( )
相切的一条直线的方程为( )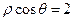

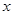 轴的非负半轴为极轴建立极坐标系,则线段
轴的非负半轴为极轴建立极坐标系,则线段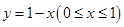 的极坐标为( )
的极坐标为( )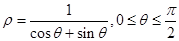
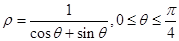

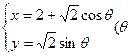 为参数),且曲线C与直线
为参数),且曲线C与直线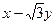 =0相交于两点A、B求弦AB的长。
=0相交于两点A、B求弦AB的长。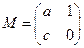 的一个特征值为
的一个特征值为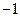 ,它对应的一个特征向量
,它对应的一个特征向量 。
。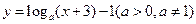 的图象恒过定点
的图象恒过定点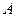 ,若点
,若点 线
线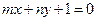 上,其中
上,其中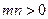 ,求
,求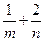 的最小值。
的最小值。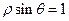 与圆
与圆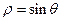 的交点坐标是__________.
的交点坐标是__________.