题目内容
(本题满分12分)
如图的多面体是底面为平行四边形的直四棱柱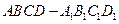 ,经平面
,经平面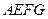 所截后得到的图形.其中
所截后得到的图形.其中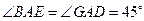 ,
,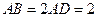 ,
,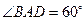 .
.
(1)求证: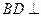 平面
平面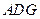 ;
;
(2)求平面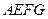 与平面
与平面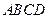 所成锐二面角的余弦值.
所成锐二面角的余弦值.
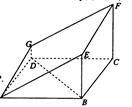
如图的多面体是底面为平行四边形的直四棱柱
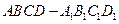 ,经平面
,经平面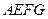 所截后得到的图形.其中
所截后得到的图形.其中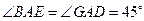 ,
,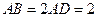 ,
,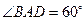 .
.(1)求证:
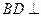 平面
平面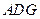 ;
; (2)求平面
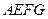 与平面
与平面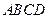 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(1) 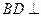 平面
平面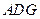
(2)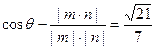
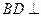 平面
平面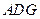
(2)
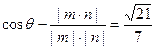
(1)证明:在△BAD中,AB=2AD=2,∠BAD=60°,
由余弦定理得,BD=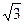
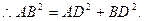
∴AD⊥BD……………………2分
又OD⊥平面ABCD
∴GD⊥BD,
GD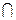 AD=D,
AD=D,
∴BD⊥平面ADG……………………4分
(2)解:以D为坐标原点,建立如图所示的空间直角坐标系D—xyz
则有A(1,0,0),B(0,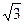 ,0),G(0,0,1),E(0,
,0),G(0,0,1),E(0,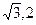 )
)
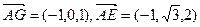 ………………6分
………………6分
设平面AEFG法向量为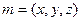
则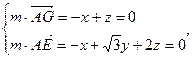
取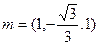 …………………………9分
…………………………9分
平面ABCD的一个法向量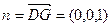 ………………10分
………………10分
设面ABFG与面ABCD所成锐二面角为 ,
,
则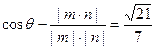 ……………………12分
……………………12分
由余弦定理得,BD=
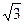
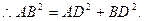
∴AD⊥BD……………………2分
又OD⊥平面ABCD
∴GD⊥BD,
GD
 AD=D,
AD=D,∴BD⊥平面ADG……………………4分
(2)解:以D为坐标原点,建立如图所示的空间直角坐标系D—xyz
则有A(1,0,0),B(0,
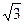 ,0),G(0,0,1),E(0,
,0),G(0,0,1),E(0,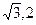 )
)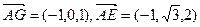 ………………6分
………………6分设平面AEFG法向量为
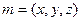
则
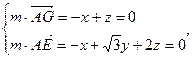
取
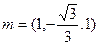 …………………………9分
…………………………9分平面ABCD的一个法向量
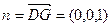 ………………10分
………………10分设面ABFG与面ABCD所成锐二面角为
 ,
,则
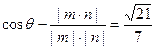 ……………………12分
……………………12分
练习册系列答案
相关题目
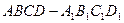 中,
中,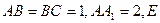 是侧棱
是侧棱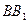 的中点 ,
的中点 , 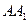 与平面
与平面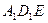 所成的角的大小;
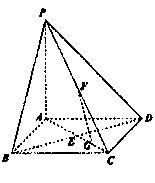
所成的角的大小; 的体积;
的体积;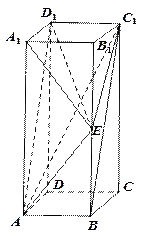
 是两条不同的直线,
是两条不同的直线,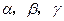 是三个不同的平面,则下列命题中的真命题是( )
是三个不同的平面,则下列命题中的真命题是( )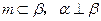 ,则
,则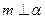
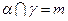
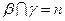 ,
,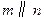 ,则
,则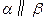
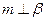 ,
,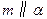 ,则
,则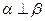
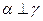 ,
,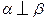 ,则
,则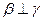
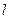 ⊥平面
⊥平面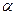 ,直线
,直线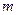
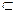 平面
平面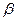 ,给出下列四个命题:
,给出下列四个命题: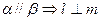 ②
②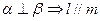 ③
③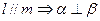 ④
④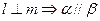
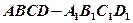 的侧面
的侧面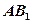 内 有一点
内 有一点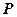 ,它到直线
,它到直线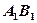 与到直线
与到直线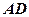 的距离相等,则动点
的距离相等,则动点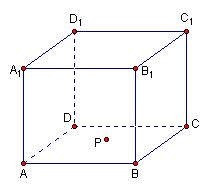
 BC,PC
BC,PC