题目内容
(13分)
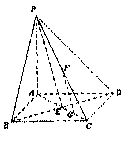
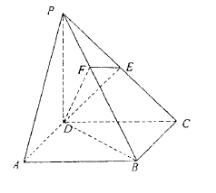
如图,在底面是正方形的四棱锥P—ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
(I)求证:BD⊥FG;
(II)确定点G在线段AC上的位置,使FG//平面PBD,并说明理由.
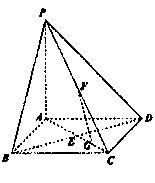
如图,在底面是正方形的四棱锥P—ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
(I)求证:BD⊥FG;
(II)确定点G在线段AC上的位置,使FG//平面PBD,并说明理由.

证明:(I)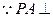 面ABCD,四边形ABCD是正方形,
面ABCD,四边形ABCD是正方形,
其对角线BD,AC交于点E,
∴PA⊥BD,AC⊥BD.
∴BD⊥平面APC,
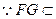 平面PAC,
平面PAC,
∴BD⊥FG …………7分
(II)当G为EC中点,即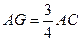 时,FG//平面PBD, …………9分
时,FG//平面PBD, …………9分
理由如下:
连接PE,由F为PC中点,G为EC中点,知FG//PE,
而FG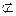 平面PBD,PB
平面PBD,PB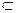 平面PBD,
平面PBD,
故FG//平面PBD. …………13分
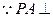 面ABCD,四边形ABCD是正方形,
面ABCD,四边形ABCD是正方形,其对角线BD,AC交于点E,
∴PA⊥BD,AC⊥BD.
∴BD⊥平面APC,
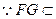 平面PAC,
平面PAC,∴BD⊥FG …………7分
|
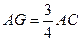 时,FG//平面PBD, …………9分
时,FG//平面PBD, …………9分理由如下:
连接PE,由F为PC中点,G为EC中点,知FG//PE,
而FG
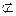 平面PBD,PB
平面PBD,PB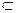 平面PBD,
平面PBD,故FG//平面PBD. …………13分
略

练习册系列答案
相关题目
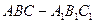 中,侧棱与底面垂直,
中,侧棱与底面垂直,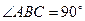 ,
,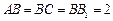 ,
, 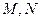 分别是
分别是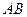 ,
,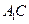 的中点.
的中点.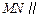 平面
平面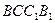 ;
; 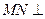 平面
平面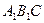 ;
;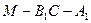 的余弦值.
的余弦值.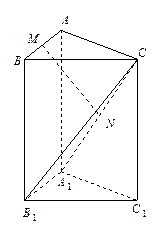
 ,E为SD的中点。
,E为SD的中点。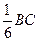 ,求证:EF∥平面SAB;
,求证:EF∥平面SAB; ?
?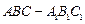 中,
中,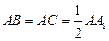 ,
,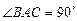 ,
,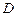 为棱
为棱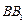 的中点.
的中点. (1)求证:
(1)求证: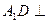 平面
平面 ;
;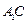 与平面ADC所成角的正弦值.
与平面ADC所成角的正弦值.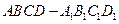 ,经平面
,经平面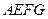 所截后得到的图形.其中
所截后得到的图形.其中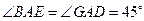 ,
,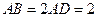 ,
,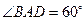 .
.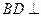 平面
平面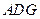 ;
; 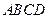 所成锐二面角的余弦值.
所成锐二面角的余弦值.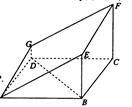
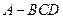 中,
中,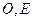 分别是
分别是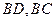 的中点,
的中点,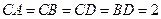 ,
,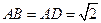 。
。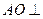 平面
平面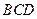 ;
;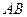 与
与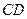 所成角的余弦值;
所成角的余弦值;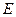 到平面
到平面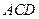 的距离。
的距离。
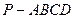 中,底面
中,底面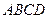 是正方形,侧棱
是正方形,侧棱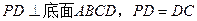 ,
,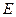 为
为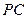 中点,作
中点,作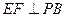 交
交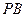 于
于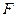
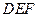 与平面
与平面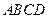 所成的锐二面角的正弦值。
所成的锐二面角的正弦值。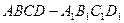 中,
中,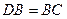 ,
, 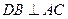 ,点
,点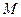 是棱
是棱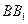 上一点.
上一点.
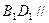 面
面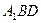 ;
;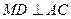 ;
;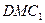
 平面
平面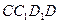 .
. 、
、 、
、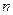 是互不相同的空间直线,
是互不相同的空间直线,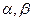 是不重合的平面,则下列命题中为真命题的是( )
是不重合的平面,则下列命题中为真命题的是( )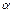 ∥β,
∥β,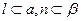 ,则
,则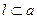 ,则
,则