题目内容
(本小题满分13分)
已知函数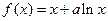 ,其中
,其中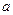 为常数,且
为常数,且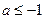 。
。
(I) 当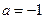 时,求
时,求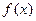 在
在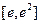 (
(
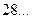 )上的值域;
)上的值域;
(II) 若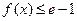 对任意
对任意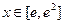 恒成立,求实数
恒成立,求实数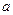 的取值范围。
的取值范围。
已知函数
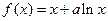 ,其中
,其中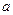 为常数,且
为常数,且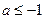 。
。(I) 当
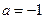 时,求
时,求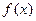 在
在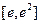 (
(
 )上的值域;
)上的值域;(II) 若
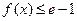 对任意
对任意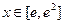 恒成立,求实数
恒成立,求实数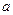 的取值范围。
的取值范围。(Ⅰ)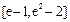 (Ⅱ)
(Ⅱ)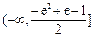
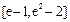 (Ⅱ)
(Ⅱ)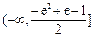
(Ⅰ)当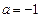 时,
时,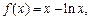
得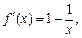 ………………2分
………………2分
令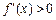 ,即
,即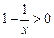 ,解得
,解得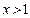 ,所以函数
,所以函数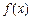 在
在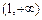 上为增函数,
上为增函数,
据此,函数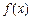 在
在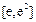 上为增函数, ………………4分
上为增函数, ………………4分
而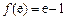 ,
,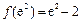 ,所以函数
,所以函数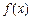 在
在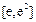 上的值域为
上的值域为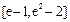
………………6分
(Ⅱ)由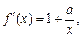 令
令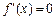 ,得
,得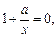 即
即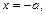
当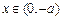 时,
时,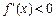 ,函数
,函数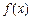 在
在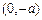 上单调递减;
上单调递减;
当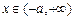 时,
时,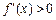 ,函数
,函数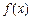 在
在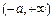 上单调递增; ……………7分
上单调递增; ……………7分
若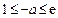 ,即
,即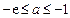 ,易得函数
,易得函数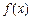 在
在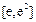 上为增函数,
上为增函数,
此时,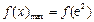 ,要使
,要使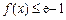 对
对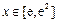 恒成立,只需
恒成立,只需 即可,
即可,
所以有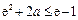 ,即
,即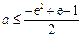
而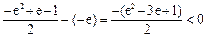 ,即
,即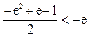 ,所以此时无解.
,所以此时无解.
………………8分
若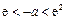 ,即
,即 ,易知函数
,易知函数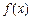 在
在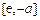 上为减函数,在
上为减函数,在 上为增函数,
上为增函数,
要使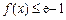 对
对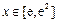 恒成立,只需
恒成立,只需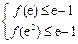 ,即
,即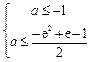 ,
,
由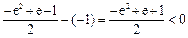 和
和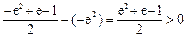
得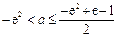 . ………………10分
. ………………10分
若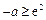 ,即
,即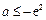 ,易得函数
,易得函数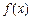 在
在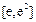 上为减函数,
上为减函数,
此时,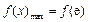 ,要使
,要使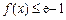 对
对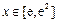 恒成立,只需
恒成立,只需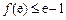 即可,
即可,
所以有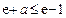 ,即
,即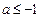 ,又因为
,又因为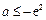 ,所以
,所以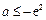 . ……………12分
. ……………12分
 综合上述,实数a的取值范围是
综合上述,实数a的取值范围是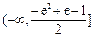 . ……………13分
. ……………13分
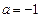 时,
时,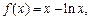
得
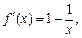 ………………2分
………………2分令
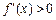 ,即
,即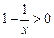 ,解得
,解得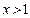 ,所以函数
,所以函数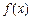 在
在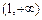 上为增函数,
上为增函数,据此,函数
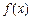 在
在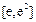 上为增函数, ………………4分
上为增函数, ………………4分而
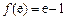 ,
,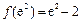 ,所以函数
,所以函数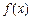 在
在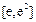 上的值域为
上的值域为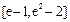
………………6分
(Ⅱ)由
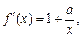 令
令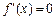 ,得
,得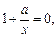 即
即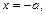
当
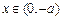 时,
时,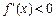 ,函数
,函数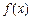 在
在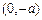 上单调递减;
上单调递减;当
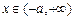 时,
时,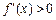 ,函数
,函数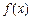 在
在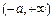 上单调递增; ……………7分
上单调递增; ……………7分若
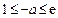 ,即
,即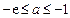 ,易得函数
,易得函数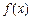 在
在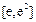 上为增函数,
上为增函数,此时,
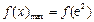 ,要使
,要使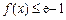 对
对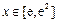 恒成立,只需
恒成立,只需 即可,
即可,所以有
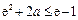 ,即
,即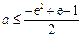
而
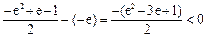 ,即
,即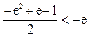 ,所以此时无解.
,所以此时无解.………………8分
若
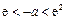 ,即
,即 ,易知函数
,易知函数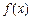 在
在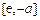 上为减函数,在
上为减函数,在 上为增函数,
上为增函数,要使
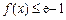 对
对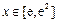 恒成立,只需
恒成立,只需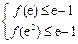 ,即
,即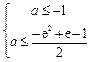 ,
,由
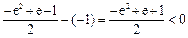 和
和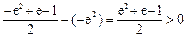
得
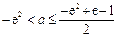 . ………………10分
. ………………10分若
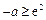 ,即
,即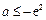 ,易得函数
,易得函数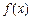 在
在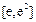 上为减函数,
上为减函数,此时,
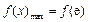 ,要使
,要使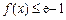 对
对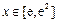 恒成立,只需
恒成立,只需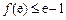 即可,
即可,所以有
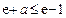 ,即
,即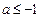 ,又因为
,又因为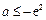 ,所以
,所以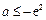 . ……………12分
. ……………12分 综合上述,实数a的取值范围是
综合上述,实数a的取值范围是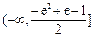 . ……………13分
. ……………13分
练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
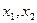 是函数
是函数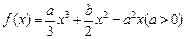 的两个极值点,且
的两个极值点,且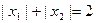
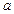 的取值范围;
的取值范围;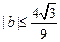 .
.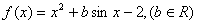 ,且对任意
,且对任意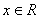 ,有
,有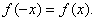
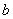 。
。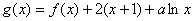 在区间(0,1)上为单调函数,求实数
在区间(0,1)上为单调函数,求实数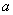 的取值范围。
的取值范围。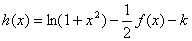 的零点个数?
的零点个数?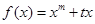 的导数
的导数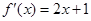 ,则数列
,则数列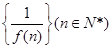 的前n项
的前n项
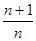


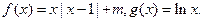 (1)当
(1)当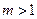 时,求函数
时,求函数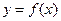 在
在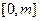 上的最大值;(2)记函数
上的最大值;(2)记函数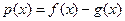 ,若函数
,若函数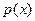 有零点,求
有零点,求 的取值范围.
的取值范围.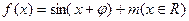 为奇函数,且过点
为奇函数,且过点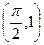 ,函数
,函数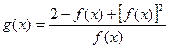 .
.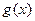 的解析式并求其定义域;
的解析式并求其定义域;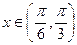 时不等式
时不等式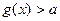 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.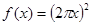 的导数是( )
的导数是( )



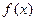 满足:
满足: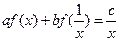 (其中a、b、c均为常数,且|a|≠|b|),试求
(其中a、b、c均为常数,且|a|≠|b|),试求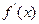 .
. 的解析式可能是( )
的解析式可能是( )


