题目内容
为了对某课题进行研究,用分层抽样方法从三所科研单位A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人):
| 科研单位 | 相关人数 | 抽取人数 |
| A | 16 |  |
| B | 12 | 3 |
| C | 8 | 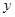 |
 与
与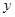 的值;
的值;(Ⅱ)若从科研单位A、C抽取的人中选2人作专题发言,求这2人都来自科研单位A的概率.
(Ⅰ)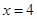 ,
, ;
;
(Ⅱ)选中的2人都来自科研单位A的概率为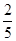 .
.
解析试题分析:(Ⅰ)确定 与
与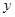 的值,由分层抽样的特点,是按比例抽样,首先计算出各层抽样比,由B中12人抽出3人,故抽样比4:1,可根据抽样比计算出
的值,由分层抽样的特点,是按比例抽样,首先计算出各层抽样比,由B中12人抽出3人,故抽样比4:1,可根据抽样比计算出 与
与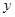 的值;(Ⅱ)若从科研单位A、C抽取的人中选2人作专题发言,求这2人都来自科研单位A的概率,由(Ⅰ)可知,从科研单位A中抽取4人,从科研单位C中抽取2人,从这6人中选2人作专题发言,求这2人都来自科研单位A的概率,显然符合古典概率的特点,首先计算出从这6人中选2人作专题发言的基本事件数,再计算出这2人都来自科研单位A的基本事件数,由古典概率的求法可求得.
的值;(Ⅱ)若从科研单位A、C抽取的人中选2人作专题发言,求这2人都来自科研单位A的概率,由(Ⅰ)可知,从科研单位A中抽取4人,从科研单位C中抽取2人,从这6人中选2人作专题发言,求这2人都来自科研单位A的概率,显然符合古典概率的特点,首先计算出从这6人中选2人作专题发言的基本事件数,再计算出这2人都来自科研单位A的基本事件数,由古典概率的求法可求得.
试题解析:(Ⅰ)依题意得,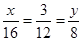 ,解得
,解得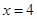 ,
, . 5分
. 5分
(Ⅱ)记从科研单位A抽取的4人为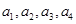 ,从科研单位C抽取的2人为
,从科研单位C抽取的2人为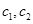 ,则从科研单位A、C抽取的6人中选2人作专题发言的基本事件有:
,则从科研单位A、C抽取的6人中选2人作专题发言的基本事件有: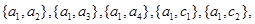
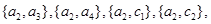
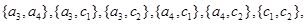 共15种. 8分
共15种. 8分
记“选中的2人都来自科研单位A”为事件 ,则事件
,则事件 包含的基本事件有:
包含的基本事件有: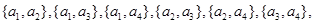 共6种. 11分
共6种. 11分
则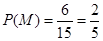 .所以选中的2人都来自科研单位A的概率为
.所以选中的2人都来自科研单位A的概率为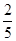 12分
12分
考点:分层抽样,古典概率.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案某学校100名学生期中考试语文成绩的频率分布直方图如下右图所示,其中成绩分组区间是: ,
,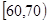 ,
, ,
,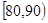 ,
, 。
。
求图中a的值;
根据频率分布直方图,估计这100名学生语文成绩的平均分;
若这100名学生语文成绩某些分数段的人数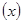 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数
之比如下表所示,求数学成绩在 之外的人数。
之外的人数。
| 分数段 |  | 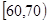 |  | 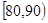 |
x :y :y | 1:1 | 2:1 | 3:4 | 4:5 |
某同学在生物研究性学习中,对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究,于是他在4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下资料:
| 日 期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 颗 颗 | 23 | 25 | 30 | 26 | 16 |
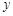 关于
关于 的线性回归方程
的线性回归方程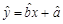 ;
;(Ⅱ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(Ⅰ)中所得的线性回归方程是否可靠?
(参考公式:
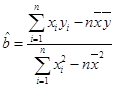
 ,
, )
)(参考数据:
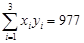 ,
, )
) 为了调查某大学学生在周日上网的时间,随机对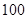 名男生和
名男生和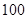 名女生进行了不记名的问卷调查,得到了如下的统计结果:
名女生进行了不记名的问卷调查,得到了如下的统计结果:
表1:男生上网时间与频数分布表
| 上网时间(分钟) | 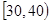 | 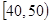 | 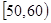 |  | 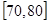 |
| 人数 | 5 | 25 | 30 | 25 | 15 |
| 上网时间(分钟) | 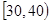 | 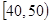 | 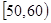 |  | 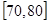 |
| 人数 | 10 | 20 | 40 | 20 | 10 |
(Ⅱ)完成表3的
 列联表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?
列联表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?(Ⅲ)从表3的男生中“上网时间少于60分钟”和“上网时间不少于60分钟”的人数中用分层抽样的方法抽取一个容量为5的样本,再从中任取两人,求至少有一人上网时间超过60分钟的概率.
表3 :
| | 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 |
| 男生 | | | |
| 女生 | | | |
| 合计 | | | |
 ,其中
,其中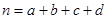
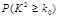 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
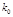 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
 名同学,现测得排球队
名同学,现测得排球队 )分别是:
)分别是: 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、
 (简称血酒含量,单位是毫克/
(简称血酒含量,单位是毫克/ 毫升),当
毫升),当 时,为“酒后驾车”;当
时,为“酒后驾车”;当 时,为“醉酒驾车”.某市公安局交通管理部门于
时,为“醉酒驾车”.某市公安局交通管理部门于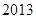 年
年 月的某天晚上
月的某天晚上 点至
点至 名饮酒后违法驾驶机动车者,如图为这
名饮酒后违法驾驶机动车者,如图为这 的人数计入
的人数计入 人数之内).
人数之内).
 人,求
人,求 人为“酒后驾车”另
人为“酒后驾车”另 户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)
户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)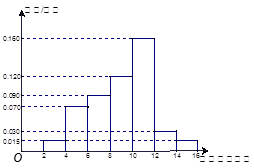
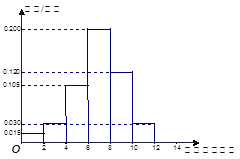
 户,在政府进行节水动员前平均每月用水量是
户,在政府进行节水动员前平均每月用水量是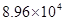 吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;
吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;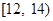 内的家庭中选出
内的家庭中选出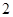 户作为采访对象,其中甲、乙两家在备选之列,求恰好选中他们两家作为采访对象的概率
户作为采访对象,其中甲、乙两家在备选之列,求恰好选中他们两家作为采访对象的概率  上,将这些成绩分成六段
上,将这些成绩分成六段 ,
, ,…
,… ,后得到如图所示部分频率分布直方图.
,后得到如图所示部分频率分布直方图.
 内的人数;(5分)
内的人数;(5分)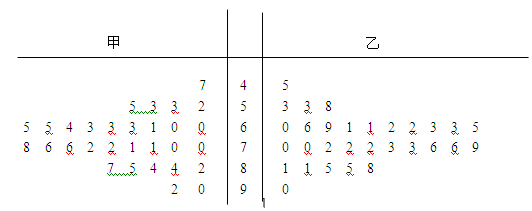
 ,估计
,估计 的值.
的值.