题目内容
某学校100名学生期中考试语文成绩的频率分布直方图如下右图所示,其中成绩分组区间是: ,
,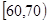 ,
, ,
,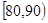 ,
, 。
。
求图中a的值;
根据频率分布直方图,估计这100名学生语文成绩的平均分;
若这100名学生语文成绩某些分数段的人数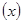 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数
之比如下表所示,求数学成绩在 之外的人数。
之外的人数。
| 分数段 |  | 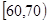 |  | 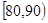 |
x :y :y | 1:1 | 2:1 | 3:4 | 4:5 |
(1)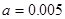 ; (2)73; (3)10
; (2)73; (3)10
解析试题分析:(1)由频率分布直方图的性质可10(2a+0.02+0.03+0.04)=1,解方程即可得到a的值;(2)由平均数加权公式可得平均数为55×0.05+65×0.4+75×0.3+85×0.2+95×0.05,计算出结果既得.(3)先求出数学成绩在[50,90)之内的人数,用100减去此数,得出结果.解题的关键是理解频率分布直方图,熟练掌握频率分布直方图的性质,且能根据所给的数据建立恰当的方程求解.
试题解析:(1)、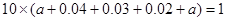 2分
2分
解得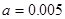 3分
3分
(2)、50-60段语文成绩的人数为: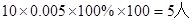
60-70段语文成绩的人数为: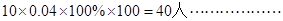 4分
4分
70-80段语文成绩的人数为: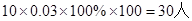
80-90段语文成绩的人数为: 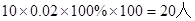
90-100段语文成绩的人数为: 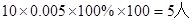 5分
5分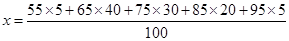 7分
7分
=73 8分
(3)、依题意:
50-60段数学成绩的人数=50-60段语文成绩的人数为=5人 9分
60-70段数学成绩的的人数为=50-60段语文成绩的人数的一半=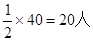 10分
10分
70-80段数学成绩的的人数为=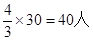 11分
11分
80-90段数学成绩的的人数为=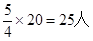 12分
12分
90-100段数学成绩的的人数为=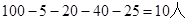 13分
13分
考点:1.考查频率分布估计总体分布;2.频率分布直方图.

据《中国新闻网》10月21日报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改”引起广泛关注.为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查(若所选择的在校学生的人数低于被调查人群总数的80%,则认为本次调查“失效”),就“是否取消英语听力”的问题,调查统计的结果如下表:
| 应该取消 | 应该保留 | 无所谓 | ||
| 在校学生 | 2100人 | 120人 | y人 | ||
| 社会人士 | 600人 | x人 | z人 |
(Ⅰ)现用分层抽样的方法在所有参与调查的人中抽取360人进行深入访谈,问应在持“无所谓”态度的人中抽取多少人?
(Ⅱ)已知y≥657,z≥55,求本次调查“失效”的概率.
为预防H7N9病毒爆发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如下表:
| 分组 | A组 | B组 | C组 |
| 疫苗有效 | 673 | a | b |
| 疫苗无效 | 77 | 90 | c |
(I)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取样本多少个?
(II)已知b≥465,c ≥30,求通过测试的概率
改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村2001到2005年五年间每年考入大学的人数,为了方便计算,2001年编号为1,2002年编号为2,……,2005年编号为5,数据如下:
| 年份(x) | 1 | 2 | 3 | 4 | 5 |
| 人数(y) | 3 | 5 | 8 | 11 | 13 |
 年多于10人的概率.
年多于10人的概率.(2)根据这
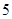 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出 关于
关于 的回归方程
的回归方程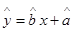 ,并计算第
,并计算第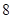 年的估计值。
年的估计值。参考:用最小二乘法求线性回归方程系数公式
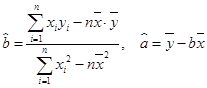
为了对某课题进行研究,用分层抽样方法从三所科研单位A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人):
| 科研单位 | 相关人数 | 抽取人数 |
| A | 16 |  |
| B | 12 | 3 |
| C | 8 | 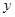 |
 与
与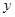 的值;
的值;(Ⅱ)若从科研单位A、C抽取的人中选2人作专题发言,求这2人都来自科研单位A的概率.
某校高三期末统一测试,随机抽取一部分学生的数学成绩分组统计如下表:
(Ⅰ)求出表中 、
、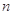 、
、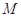 、
、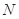 的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
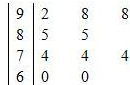
| 分组 | 频数 | 频率 |
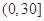 | 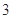 | 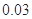 |
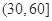 | 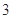 | 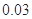 |
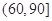 | 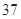 | 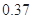 |
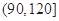 |  | 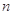 |
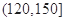 | 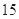 | 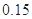 |
| 合计 | 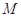 | 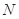 |

(Ⅱ)若全校参加本次考试的学生有600人,试估计这次测试中全校成绩在
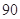 分以上的人数;
分以上的人数;(Ⅲ)若该校教师拟从分数不超过60的学生中选取2人进行个案分析,求被选中2人分数不超过30分的概率.
某校为了解高三年级不同性别的学生对体育课改上自习课的态度(肯定还是否定),进行了如下的调查研究.全年级共有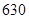 名学生,男女生人数之比为
名学生,男女生人数之比为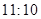 ,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为
,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为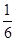 .
.
(1)求抽取的男学生人数和女学生人数;
(2)通过对被抽取的学生的问卷调查,得到如下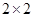 列联表:
列联表:
| | 否定 | 肯定 | 总计 |
| 男生 | | 10 | |
| 女生 | 30 | | |
| 总计 | | | |
②能否有
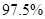 的把握认为态度与性别有关?
的把握认为态度与性别有关?(3)若一班有
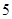 名男生被抽到,其中
名男生被抽到,其中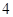 人持否定态度,
人持否定态度, 人持肯定态度;二班有
人持肯定态度;二班有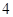 名女生被抽到,其中
名女生被抽到,其中 人持否定态度,
人持否定态度, 人持肯定态度.
人持肯定态度.现从这
 人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.
人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.解答时可参考下面临界值表:
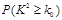 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
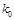 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
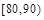 、
、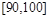 上的概率.
上的概率.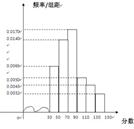
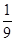 ,求甲在初赛中答题个数的分布列及数学期望.
,求甲在初赛中答题个数的分布列及数学期望.