题目内容
 (2013•怀化二模)如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD=
(2013•怀化二模)如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD=| 2 |
(Ⅰ)求证:AO⊥平面BCD;
(Ⅱ)求异面直线AB与CD所成角的余弦;
(Ⅲ)求点E到平面ACD的距离.
分析:(I)连接OC,由BO=DO,AB=AD,知AO⊥BD,由BO=DO,BC=CD,知CO⊥BD.在△AOC中,由题设知AO=1,CO=
,AC=2,故AO2+CO2=AC2,由此能够证明AO⊥平面BCD.
(II)取AC的中点M,连接OM、ME、OE,由E为BC的中点,知ME∥AB,OE∥DC,故直线OE与EM所成的锐角就是异面直线AB与CD所成的角.在△OME中,EM=
AB=
,OE=
DC=1,由此能求出异面直线AB与CD所成角大小的余弦.
(III)设点E到平面ACD的距离为h.在△ACD中,CA=CD=2,AD=
,故S△ACD=
×
×
=
,由AO=1,知S△CDE=
×
×22=
,由此能求出点E到平面ACD的距离.
| 3 |
(II)取AC的中点M,连接OM、ME、OE,由E为BC的中点,知ME∥AB,OE∥DC,故直线OE与EM所成的锐角就是异面直线AB与CD所成的角.在△OME中,EM=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
(III)设点E到平面ACD的距离为h.在△ACD中,CA=CD=2,AD=
| 2 |
| 1 |
| 2 |
| 2 |
4-(
|
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| ||
| 2 |
解答: (I)证明:连接OC,∵BO=DO,AB=AD,∴AO⊥BD,
(I)证明:连接OC,∵BO=DO,AB=AD,∴AO⊥BD,
∵BO=DO,BC=CD,∴CO⊥BD.
在△AOC中,由题设知AO=1,CO=
,AC=2,
∴AO2+CO2=AC2,
∴∠AOC=90°,即AO⊥OC.
∵AO⊥BD,BD∩OC=O,
∴AO⊥平面BCD.
(II)解:取AC的中点M,连接OM、ME、OE,由E为BC的中点,
知ME∥AB,OE∥DC,
∴直线OE与EM所成的锐角就是异面直线AB与CD所成的角.
在△OME中,EM=
AB=
,OE=
DC=1,…(6分)
∵OM是直角△AOC斜边AC上的中线,∴OM=
AC=1,…(7分)
∴cos∠OEM=
=
,
∴异面直线AB与CD所成角大小的余弦为
…(8分)
(III)解:设点E到平面ACD的距离为h.
…(9分)
在△ACD中,CA=CD=2,AD=
,
∴S△ACD=
×
×
=
,
∵AO=1,S△CDE=
×
×22=
,
∴h=
=
=
,
∴点E到平面ACD的距离为
.
 (I)证明:连接OC,∵BO=DO,AB=AD,∴AO⊥BD,
(I)证明:连接OC,∵BO=DO,AB=AD,∴AO⊥BD,∵BO=DO,BC=CD,∴CO⊥BD.
在△AOC中,由题设知AO=1,CO=
| 3 |
∴AO2+CO2=AC2,
∴∠AOC=90°,即AO⊥OC.
∵AO⊥BD,BD∩OC=O,
∴AO⊥平面BCD.
(II)解:取AC的中点M,连接OM、ME、OE,由E为BC的中点,
知ME∥AB,OE∥DC,
∴直线OE与EM所成的锐角就是异面直线AB与CD所成的角.
在△OME中,EM=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
∵OM是直角△AOC斜边AC上的中线,∴OM=
| 1 |
| 2 |
∴cos∠OEM=
| 1+1/2-1 | ||
2×1×
|
| ||
| 4 |
∴异面直线AB与CD所成角大小的余弦为
| ||
| 4 |
(III)解:设点E到平面ACD的距离为h.
|
在△ACD中,CA=CD=2,AD=
| 2 |
∴S△ACD=
| 1 |
| 2 |
| 2 |
4-(
|
| ||
| 2 |
∵AO=1,S△CDE=
| 1 |
| 2 |
| ||
| 4 |
| ||
| 2 |
∴h=
| AO•S△CDE |
| S△ACD |
1×
| ||||
|
| ||
| 7 |
∴点E到平面ACD的距离为
| ||
| 7 |
点评:本题考查点、线、面间的距离的计算,考查空间想象力和等价转化能力,解题时要认真审题,仔细解答,注意化立体几何问题为平面几何问题.

练习册系列答案
相关题目
 (2013•怀化二模)如图1,小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1,再把正方形A1B1C1D1的各边延长一倍得到正方形A2B2C2D2(如图2),如此进行下去,正方形AnBnCnDn的面积为
(2013•怀化二模)如图1,小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1,再把正方形A1B1C1D1的各边延长一倍得到正方形A2B2C2D2(如图2),如此进行下去,正方形AnBnCnDn的面积为 (2013•怀化二模)如图所示,四棱锥P-ABCD,底面ABCD是边长为2的正方形,PA⊥面ABCD,PA=2,过点A作AE⊥PB,AF⊥PC,连接EF.
(2013•怀化二模)如图所示,四棱锥P-ABCD,底面ABCD是边长为2的正方形,PA⊥面ABCD,PA=2,过点A作AE⊥PB,AF⊥PC,连接EF.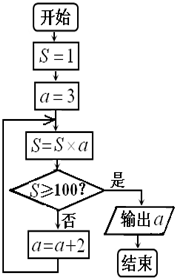 (2013•怀化二模)实数a的值由如图程序框图算出,则二项式
(2013•怀化二模)实数a的值由如图程序框图算出,则二项式