题目内容
(2013•怀化二模)如图展示了一个由区间(0,k)(其中k为一正实数)到实数集R上的映射过程:区间(0,k)中的实数m对应线段AB上的点M,如图1;将线段AB围成一个离心率为
的椭圆,使两端点A、B恰好重合于椭圆的一个短轴端点,如图2;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在x轴上,已知此时点A的坐标为(0,1),如图3,在图形变化过程中,图1中线段AM的长度对应于图3中的椭圆弧ADM的长度.图3中直线AM与直线y=-2交于点N(n,-2),则与实数m对应的实数就是n,记作f(m)=n,

现给出下列5个命题①f(
)=6;②函数f(m)是奇函数;③函数f(m)在(0,k)上单调递增;④函数f(m)的图象关于点(
,0)对称;⑤函数f(m)=3
时AM过椭圆的右焦点.其中所有的真命题是( )
| ||
| 2 |

现给出下列5个命题①f(
| k |
| 2 |
| k |
| 2 |
| 3 |
分析:本题利用直接法和排除法解决.由题意知,①可直接求解其函数值进行判断;
②函数f(x)的定义域为(0,k),不关于原点对称,函数f(x)是非奇非偶函数;
③当x从0→k变化时,点N逐渐右移,其对应的坐标值逐渐变大;
④由于当m=
时,对应的点M是椭圆的另一短轴端点,所以f(x)的图象关于点(
,0)对称;
⑤由于函数f(m)=3
,可求N点坐标,联立A点,可求直线AM,进而即可判断此时AM是否过椭圆的右焦点.
②函数f(x)的定义域为(0,k),不关于原点对称,函数f(x)是非奇非偶函数;
③当x从0→k变化时,点N逐渐右移,其对应的坐标值逐渐变大;
④由于当m=
| k |
| 2 |
| k |
| 2 |
⑤由于函数f(m)=3
| 3 |
解答:解:由题意知,①当m=
时,对应的点M是椭圆的另一短轴端点,f(
)=0,故①错误;
②∵函数f(x)的定义域为(0,4),关于原点不对称,∴函数f(x)不可能是奇函数,故②错误;
③当x从0→k变化时,点N逐渐右移,其对应的坐标值逐渐变大,故③正确;
④由于当m=
时,对应的点M是椭圆的另一短轴端点,所以f(x)的图象关于点(
,0)对称,故④正确;
⑤由于函数f(m)=3
,则N(3
,-2),故AM方程是:y=-
x+1,
又由椭圆的右焦点坐标为(
,0),所以函数f(m)=3
时AM过椭圆的右焦点,故⑤正确.
故答案为:③④⑤.
| k |
| 2 |
| k |
| 2 |
②∵函数f(x)的定义域为(0,4),关于原点不对称,∴函数f(x)不可能是奇函数,故②错误;
③当x从0→k变化时,点N逐渐右移,其对应的坐标值逐渐变大,故③正确;
④由于当m=
| k |
| 2 |
| k |
| 2 |
⑤由于函数f(m)=3
| 3 |
| 3 |
| ||
| 3 |
又由椭圆的右焦点坐标为(
| 3 |
| 3 |
故答案为:③④⑤.
点评:本题主要考查了映射和函数的概念及其构成要素,具有一定的新意,关于新定义型的题,关键是理解定义,并会用定义来解题.

练习册系列答案
相关题目
 (2013•怀化二模)如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD=
(2013•怀化二模)如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD= (2013•怀化二模)如图1,小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1,再把正方形A1B1C1D1的各边延长一倍得到正方形A2B2C2D2(如图2),如此进行下去,正方形AnBnCnDn的面积为
(2013•怀化二模)如图1,小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1,再把正方形A1B1C1D1的各边延长一倍得到正方形A2B2C2D2(如图2),如此进行下去,正方形AnBnCnDn的面积为 (2013•怀化二模)如图所示,四棱锥P-ABCD,底面ABCD是边长为2的正方形,PA⊥面ABCD,PA=2,过点A作AE⊥PB,AF⊥PC,连接EF.
(2013•怀化二模)如图所示,四棱锥P-ABCD,底面ABCD是边长为2的正方形,PA⊥面ABCD,PA=2,过点A作AE⊥PB,AF⊥PC,连接EF.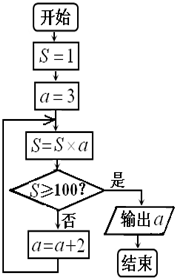 (2013•怀化二模)实数a的值由如图程序框图算出,则二项式
(2013•怀化二模)实数a的值由如图程序框图算出,则二项式