题目内容
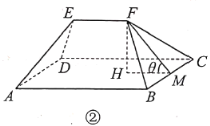
【题目】![]() 市实施全域旅游,将乡村旅游公路建设与特色田园乡村发展结合,精心打造全长365公里的“1号公路”,对内串联区域内主要景区景点和自然村,对外通达周边县(市),以路引景、为景串线,形成一个“大环小圈、内连外引”的路网体系.如今的“1号公路”,不仅成为该市旅游业的“颜值担当”,更成为推动乡村振兴的“实力担当”,农村居住环境日益改善,新农村别墅随处可见.图①是一栋新农村别墅,它由上部屋顶和下部主体两部分组成.如图②,屋顶由四坡屋面构成,其中前后两坡屋面
市实施全域旅游,将乡村旅游公路建设与特色田园乡村发展结合,精心打造全长365公里的“1号公路”,对内串联区域内主要景区景点和自然村,对外通达周边县(市),以路引景、为景串线,形成一个“大环小圈、内连外引”的路网体系.如今的“1号公路”,不仅成为该市旅游业的“颜值担当”,更成为推动乡村振兴的“实力担当”,农村居住环境日益改善,新农村别墅随处可见.图①是一栋新农村别墅,它由上部屋顶和下部主体两部分组成.如图②,屋顶由四坡屋面构成,其中前后两坡屋面![]() 和
和![]() 是全等的等腰梯形,左右两坡屋面
是全等的等腰梯形,左右两坡屋面![]() 和
和![]() 是全等的三角形.点
是全等的三角形.点![]() 在平面
在平面![]() 和
和![]() 上的射影分别为
上的射影分别为![]() (即:
(即:![]() 平面
平面![]() ,垂足为
,垂足为![]() ;
;![]() ,垂足为
,垂足为![]() ).已知
).已知![]() ,梯形
,梯形![]() 的面积是
的面积是![]() 面积的2.2倍.
面积的2.2倍.![]() .
.

(1)当![]() 时,求屋顶面积的大小;
时,求屋顶面积的大小;
(2)求屋顶面积![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)已知上部屋顶造价与屋顶面积成正比,比例系数为![]() (
(![]() 为正的常数),下部主体造价与其高度成正比,比例系数为
为正的常数),下部主体造价与其高度成正比,比例系数为![]() .现欲造一栋上、下总高度为
.现欲造一栋上、下总高度为![]() 的别墅,试问:当
的别墅,试问:当![]() 为何值时,总造价最低?
为何值时,总造价最低?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)首先根据已知得到![]() ,根据
,根据![]() 得到
得到![]() ,再计算屋顶面积即可.
,再计算屋顶面积即可.
(2)首先利用![]() 表示出
表示出![]() ,从而得到
,从而得到![]() 的面积为
的面积为![]() ,再由已知条件即可得到屋顶面积
,再由已知条件即可得到屋顶面积![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(3)首先根据题意得到:别墅总造价为![]() ,再利用换元法和三角函数的性质即可得到最小值.
,再利用换元法和三角函数的性质即可得到最小值.
(1)由题意![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,得
,得![]() .
.
在![]() 中,
中,![]() ,
,
所以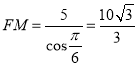 .
.
因此![]() 的面积为
的面积为![]() .
.
则屋顶面积![]()
(2)在![]() 中,
中,![]() ,
,
所以![]() .
.
因此![]() 的面积为
的面积为![]() .
.
从而屋顶面积![]() .
.
所以屋顶面积![]() 关于
关于![]() 的函数关系式
的函数关系式![]() .
.
(3)在![]() 中,
中,![]() ,所以主体高度为
,所以主体高度为![]() .
.
所以别墅总造价为![]()
![]()
![]() .
.
令![]() ,则
,则![]() .
.
设![]() ,由三角函数定义可知点
,由三角函数定义可知点![]() 是单位圆上一个动点,
是单位圆上一个动点,
可知![]() 为经过点
为经过点![]() 与点
与点![]() 的直线的斜率.
的直线的斜率.
直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
因为直线![]() 与单位圆相切或相交,
与单位圆相切或相交,
所以单位圆圆心![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
所以![]() ,解得
,解得![]() 或
或![]() .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
所以![]() ,
,
当且仅当![]() 时取“
时取“![]() ”
”
此时![]() ,即
,即![]() .
.
因为![]() ,因为
,因为![]() .
.
即![]() 时
时![]() 有最小值.
有最小值.
答:当![]() 时,总造价最低.
时,总造价最低.

【题目】从某电子商务平台随机抽取了1000位网上购物者(年消费都达到2000元),并对他们的年龄进行了调查,统计情况如下表所示:
年龄 |
|
|
|
|
|
|
人数 | 100 | 150 | 400 | 200 | 100 | 50 |
该电子商务平台将年龄在![]() 的人群定义为消费主力军,其它年龄段定义为消费潜力军.
的人群定义为消费主力军,其它年龄段定义为消费潜力军.
(1)若该电子商务平台共10万位网上购物者,试估计消费主力军的人数;
(2)为了鼓励消费潜力军消费,该平台决定对年消费达到2000元的购物者发放代金券,消费主力军每人发放100元,消费潜力军每人发放200元.现采用分层抽样(按消费主力军与消费潜力军分层)的方式从参与调查的1000位网上购物者中抽取10人,并在这10人中随机抽取3人进行回访,求这3人获得代金券总金额![]() (单位:元)的分布列及数学期望.
(单位:元)的分布列及数学期望.