题目内容
【题目】直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,已知
两点,已知![]()
![]() ,
,![]()
![]() ,若椭圆的离心率
,若椭圆的离心率![]() ,又经过点
,又经过点![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆的方程;
(2)当![]() 时,试问:
时,试问:![]() 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
【答案】(1)![]() ;(2)定值1.
;(2)定值1.
【解析】
(1)将点![]() 代入椭圆方程,结合双曲线的离心率
代入椭圆方程,结合双曲线的离心率![]() 列方程,求得
列方程,求得![]() 的值,即求得椭圆方程.(2)当直线
的值,即求得椭圆方程.(2)当直线![]() 斜率不存在时,求得三角形的面积为定值
斜率不存在时,求得三角形的面积为定值![]() .当直线
.当直线![]() 斜率存在时,设出直线
斜率存在时,设出直线![]() 的方程,联立直线方程与椭圆方程,写出韦达定理,代入
的方程,联立直线方程与椭圆方程,写出韦达定理,代入![]() ,化简.然后通过计算三角形的面积,由此判断三角形的面积为定值
,化简.然后通过计算三角形的面积,由此判断三角形的面积为定值![]() .
.
(1)∵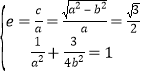 ∴
∴![]()
∴椭圆的方程为![]()
(2)①当直线![]() 斜率不存在时,即
斜率不存在时,即![]() ,
,
由已知![]()
![]() ,得
,得![]()
又![]() 在椭圆上, 所以
在椭圆上, 所以 ![]()
![]() ,三角形的面积为定值.
,三角形的面积为定值.
②当直线![]() 斜率存在时:设
斜率存在时:设![]() 的方程为
的方程为![]()
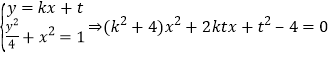
必须![]() 即
即![]() 得到
得到![]() ,
,![]()
∵![]() ,∴
,∴![]()
代入整理得:![]()
![]()
![]() 所以三角形的面积为定值.
所以三角形的面积为定值.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
