题目内容
已知m=(2cos x+2 sin x,1),n=(cos x,-y),且m⊥n.
sin x,1),n=(cos x,-y),且m⊥n.
(1)将y表示为x的函数f(x),并求f(x)的单调增区间;
(2)已知a,b,c分别为△ABC的三个内角A,B,C对应的边长,若f =3,且a=2,b+c=4,求△ABC的面积.
=3,且a=2,b+c=4,求△ABC的面积.
 sin x,1),n=(cos x,-y),且m⊥n.
sin x,1),n=(cos x,-y),且m⊥n.(1)将y表示为x的函数f(x),并求f(x)的单调增区间;
(2)已知a,b,c分别为△ABC的三个内角A,B,C对应的边长,若f
 =3,且a=2,b+c=4,求△ABC的面积.
=3,且a=2,b+c=4,求△ABC的面积.(1)  ,k∈Z. (2)
,k∈Z. (2) 
 ,k∈Z. (2)
,k∈Z. (2) 
(1)由m⊥n,得m·n=2cos 2x+2 sin xcos x-y=0,即y=2cos2x+2
sin xcos x-y=0,即y=2cos2x+2 sin xcos x=cos 2x+
sin xcos x=cos 2x+ sin 2x+1=2sin
sin 2x+1=2sin +1,∴由-
+1,∴由-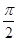 +2kπ≤2x+
+2kπ≤2x+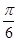 ≤
≤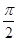 +2kπ,k∈Z,得-
+2kπ,k∈Z,得- +kπ≤x≤
+kπ≤x≤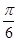 +kπ,k∈Z,即函数f(x)的增区间为
+kπ,k∈Z,即函数f(x)的增区间为 ,k∈Z.
,k∈Z.
(2)因为f =3,所以2sin
=3,所以2sin 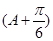 +1=3.即sin
+1=3.即sin 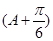 =1,
=1,
∴A+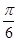 =
=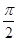 +2kπ,k∈Z又0<A<π,∴A=
+2kπ,k∈Z又0<A<π,∴A= ,由余弦定理,得
,由余弦定理,得
a2=b2+c2-2bccos A,即4=b2+c2-bc,∴4=(b+c)2-3bc,又b+c=4,
∴bc=4,∴S△ABC=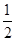 bcsin A=
bcsin A=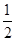 ×4×
×4×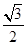 =
= .
.
 sin xcos x-y=0,即y=2cos2x+2
sin xcos x-y=0,即y=2cos2x+2 sin xcos x=cos 2x+
sin xcos x=cos 2x+ sin 2x+1=2sin
sin 2x+1=2sin +1,∴由-
+1,∴由-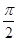 +2kπ≤2x+
+2kπ≤2x+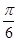 ≤
≤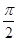 +2kπ,k∈Z,得-
+2kπ,k∈Z,得- +kπ≤x≤
+kπ≤x≤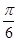 +kπ,k∈Z,即函数f(x)的增区间为
+kπ,k∈Z,即函数f(x)的增区间为 ,k∈Z.
,k∈Z.(2)因为f
 =3,所以2sin
=3,所以2sin 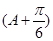 +1=3.即sin
+1=3.即sin 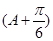 =1,
=1,∴A+
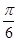 =
=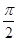 +2kπ,k∈Z又0<A<π,∴A=
+2kπ,k∈Z又0<A<π,∴A= ,由余弦定理,得
,由余弦定理,得a2=b2+c2-2bccos A,即4=b2+c2-bc,∴4=(b+c)2-3bc,又b+c=4,
∴bc=4,∴S△ABC=
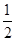 bcsin A=
bcsin A=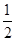 ×4×
×4×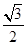 =
= .
.
练习册系列答案
相关题目
 的部分图像如图Z3-4所示,将y=f(x)的图像向右平移
的部分图像如图Z3-4所示,将y=f(x)的图像向右平移 个单位长度后得到函数y=g(x)的图像.
个单位长度后得到函数y=g(x)的图像.
 =gC+
=gC+ +1,且其外接圆半径R=2,求△ABC的面积的最大值.
+1,且其外接圆半径R=2,求△ABC的面积的最大值. 的图像向右平移
的图像向右平移 个单位,再向上平移1个单位,所得到函数的图像对应的解析式为 ( )
个单位,再向上平移1个单位,所得到函数的图像对应的解析式为 ( )



 图象的一条对称轴是( ).
图象的一条对称轴是( ).

 ,原点O到弦AP的长为d,则函数d=f(
,原点O到弦AP的长为d,则函数d=f(

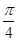 时,函数f(x)=Asin (x+φ)(A>0)取得最小值,则函数y=f
时,函数f(x)=Asin (x+φ)(A>0)取得最小值,则函数y=f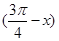 是( ).
是( ).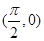 对称
对称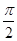 对称
对称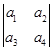 =a1a4-a2a3.将函数f(x)=
=a1a4-a2a3.将函数f(x)= 的图象向左平移
的图象向左平移 个单位,以下是所得函数图象的一个对称中心是 ( ).
个单位,以下是所得函数图象的一个对称中心是 ( ).



 (
( )的图象向右平移
)的图象向右平移 个单位后与函数
个单位后与函数 的图象重合,则
的图象重合,则 的值可能是( )
的值可能是( )
 )的图像可由曲线y=1+cos2x向左平移
)的图像可由曲线y=1+cos2x向左平移 个单位得到;②函数y=sin(x+
个单位得到;②函数y=sin(x+ )+cos(x+
)+cos(x+ 是曲线y=sin(2x+
是曲线y=sin(2x+ )的一条对称轴;④函数y=2sin2(x+
)的一条对称轴;④函数y=2sin2(x+