题目内容
5.已知a,b,c分别是△ABC的内角A,B,C所对的边,且C=$\frac{π}{3}$.(Ⅰ)若c=2,△ABC的面积S=$\sqrt{3}$,求a,b.
(Ⅱ)若cos(B-A)+cosC+2cos2A=2,求A.
分析 (I)利用三角形面积计算公式、余弦定理即可得出;
(II)利用两角和差的余弦公式、正弦定理余弦定理即可得出.
解答 解:(Ⅰ)由题意$\frac{1}{2}absin\frac{π}{3}$=$\sqrt{3}$,即ab=4,
由余弦定理c2=a2+b2-2abcosC,
∴a2+b2-ab=4,
联立$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}-ab=4}\\{ab=4}\end{array}\right.$,解得a=2,b=2;
(Ⅱ)∵cosC=-cos(B+A),
∴cos(B-A)-cos(A+B)=2-2cos2A,
∴2sinBsinA=4sin2A,
即sinB=2sinA,
由正弦定理得b=2a,
由余弦定理c2=a2+b2-2ab$cos\frac{π}{3}$=3a2,
∴b2=a2+c2,B=$\frac{π}{2}$,
∵C=$\frac{π}{3}$,
∴A=$\frac{π}{6}$.
点评 本题考查了三角形面积计算公式、两角和差的余弦公式、正弦定理余弦定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
10.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是( )
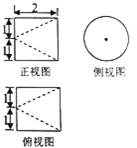

| A. | $\frac{π}{3}$cm3 | B. | $\frac{2π}{3}$cm3 | C. | πcm3 | D. | $\frac{4π}{3}$cm3 |
 已知一个空间几何体的所有棱长均为1cm,其表面展开图如图所示,则该空间几何体的体积V=$1+\frac{{\sqrt{2}}}{6}$cm3.
已知一个空间几何体的所有棱长均为1cm,其表面展开图如图所示,则该空间几何体的体积V=$1+\frac{{\sqrt{2}}}{6}$cm3. 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.