题目内容
7．函数f（x）=log3（3+2x-x2）的定义域是{x|-1＜x＜3}．分析 根据对数函数成立的条件解不等式即可．
解答 解：由3+2x-x2＞0得x2-2x-3＜0，
解得-1＜x＜3，
故函数的定义域为{x|-1＜x＜3}，
故答案为：{x|-1＜x＜3}
点评 本题主要考查函数的定义域的求解，要求熟练掌握常见函数成立的条件．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
在三棱柱ABC-A1B1C1中，AA1⊥BC，A1B⊥AC．D，E分别是BB1，A1C1的中点．
某校对学生的上学时间进行了统计（单位：分钟），并将所得数据绘制成频率分布直方图，若用分层抽样的方法从该校400名学生中抽取一个容量为20的样本，设m，n表示某两名学生的上学所需时间，且已知m，n∈[40，60）∪[80，100]，则事件|m-n|＜20的概率为$\frac{2}{5}$．
2．
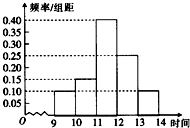某商场在今年元霄节的促销活动中，对3月5日9时至14时的销售额进行统计，其频率分布直方图如图所示．已知9时至10时的销售额为5万元，则11时至12时的销售额为（ ）
某商场在今年元霄节的促销活动中，对3月5日9时至14时的销售额进行统计，其频率分布直方图如图所示．已知9时至10时的销售额为5万元，则11时至12时的销售额为（ ）| A． | 10万元 | B． | 15万元 | C． | 20万元 | D． | 25万元 |
12．直线y=x+4与曲线y=x2-x+1所围成的封闭图形的面积为（ ）
| A． | $\frac{22}{3}$ | B． | $\frac{28}{3}$ | C． | $\frac{32}{3}$ | D． | $\frac{34}{3}$ |
如图所示，△ABC内接于⊙O，PA是⊙O的切线，PB⊥PA，BE=PE=2PD=4，则PA=4，AC=5$\sqrt{2}$．
已知一个空间几何体的所有棱长均为1cm，其表面展开图如图所示，则该空间几何体的体积V=$1+\frac{{\sqrt{2}}}{6}$cm3．