题目内容
9.对于三次函数f(x)=ax3+bx2+cx+d(a≠0),给出定义:设f′(x)是f(x)的导函数,f″(x)是f′(x)的导函数,则f′(x)叫f(x)的一阶导数,f″(x)叫f(x)的二阶导数,若方程f″x)=0有实数解x0,则称点(x0,f(x0))为函数f(x)的“拐点”.有个同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数g(x)=$\frac{1}{3}$x3-$\frac{1}{2}$x2+3x-$\frac{5}{12}$,则g($\frac{1}{2015}$)+g($\frac{2}{2015}$)+…+g($\frac{2014}{2015}$)=2014.分析 由题意求导g′(x)=x2-x+3,g″(x)=2x-1,从而得到($\frac{1}{2}$,1)是函数g(x)=$\frac{1}{3}$x3-$\frac{1}{2}$x2+3x-$\frac{5}{12}$的对称中心,从而解得.
解答 解:∵g(x)=$\frac{1}{3}$x3-$\frac{1}{2}$x2+3x-$\frac{5}{12}$,
∴g′(x)=x2-x+3,
g″(x)=2x-1,
令g″(x)=2x-1=0得,
x=$\frac{1}{2}$;
g($\frac{1}{2}$)=$\frac{1}{3}$•$\frac{1}{8}$-$\frac{1}{2}$×$\frac{1}{4}$+3×$\frac{1}{2}$-$\frac{5}{12}$=1,
则($\frac{1}{2}$,1)是函数g(x)=$\frac{1}{3}$x3-$\frac{1}{2}$x2+3x-$\frac{5}{12}$的对称中心,
则g($\frac{1}{2015}$)+g($\frac{2014}{2015}$)=2,g($\frac{2}{2015}$)+g($\frac{2013}{2015}$)=2,…,
g($\frac{1007}{2015}$)+g($\frac{1008}{2015}$)=2,
故g($\frac{1}{2015}$)+g($\frac{2}{2015}$)+…+g($\frac{2014}{2015}$)=2014;
故答案为:2014.
点评 本题考查了学生对新知识的接受与应用能力及导数的综合应用,属于中档题.

练习册系列答案
相关题目
4.从数字0,1,2,3,4,5中任取两个数组成两位数,其中奇数的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{12}{25}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
1.执行如图所示的程序框图,则输出z的值为( )
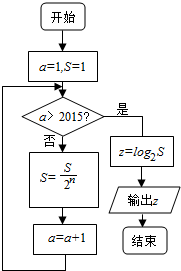

| A. | -1008×2015 | B. | 1008×2015 | C. | -1008×2017 | D. | 1008×2017 |
19.已知圆C的方程为x2+y2-2x-2y+1=0,过直线3x+4y+8=0上一点P作圆C的切线PT,切点为T,则|PT|的最小值为( )
| A. | 2$\sqrt{2}$ | B. | 3 | C. | $\sqrt{10}$ | D. | 4 |
 如图所示,△ABC内接于⊙O,PA是⊙O的切线,PB⊥PA,BE=PE=2PD=4,则PA=4,AC=5$\sqrt{2}$.
如图所示,△ABC内接于⊙O,PA是⊙O的切线,PB⊥PA,BE=PE=2PD=4,则PA=4,AC=5$\sqrt{2}$.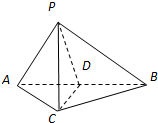 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.