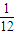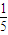Question

已知随机变量X和Y，其中Y=12X+7，且EY=34，若X的分布列如表所示，则m的值为（　　） X        1 2 3 4 P 1 4 m n 1 12

• A．

  1

  6

• B．

  1

  5

• C．

  1

  3

• D．

  1

  2

Answer 1

分析：根据随机变量X分布的概率和为1，建立m、n的等式，根据数学期望公式再建立另一等式，联立方程组解之即可求出所求．

解答：解：根据随机变量X分布的概率和为1，则

1

4

+m+n+

1

12

=1
即m+n=

2

3

       ①
EX=1×

1

4

+2m+3n+4×

1

12

=2m+3n+

7

12

∵Y=12X+7，且EY=34
∴EY=12EX+7=24m+36n+14=34     ②
联立①②得m=

1

3

故选C．

点评：本题主要考查了离散型随机变量及其分布列，以及随机变量的数学期望和二元一次方程组的解法，属于中档题．