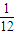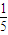Question

已知随机变量X和Y，其中Y=12X+7，且E（Y）=34，若X的概率分布如下表，则m的值为（　　） X 1 2 3 4 P 1 4 m n 1 12

• A．

  1

  3

• B．

  1

  4

• C．

  1

  6

• D．

  1

  8

Answer 1

分析：由Y=12X+7可得：EY=12EX+7，从而可求EX，利用随机变量的期望公式及所有概率和为1，联立方程，即可求得m的值

解答：解：由Y=12X+7可得：EY=12EX+7
∵EY=34
∴34=12EX+7
∴EX=

9

4

∴

9

4

=1×

1

4

+2×m+3×n+4×

1

12

，即2m+3n=

5

3

①
又

1

4

+m+n+

1

12

=1，即m+n=

2

3

②
联立①②，求解可得m=

1

3

，
故选A．

点评：本题主要考查随机变量期望的求解，考查概率的性质，属于基础题．