题目内容
已知各项均为正数的数列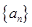 的前
的前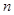 项和为
项和为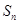 ,数列
,数列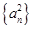 的前
的前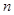 项和为
项和为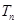 ,且
,且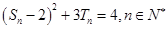 .
.
⑴证明:数列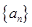 是等比数列,并写出通项公式;
是等比数列,并写出通项公式;
⑵若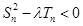 对
对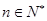 恒成立,求
恒成立,求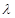 的最小值;
的最小值;
⑶若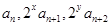 成等差数列,求正整数
成等差数列,求正整数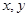 的值.
的值.
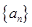 的前
的前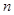 项和为
项和为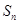 ,数列
,数列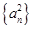 的前
的前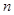 项和为
项和为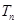 ,且
,且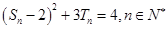 .
.⑴证明:数列
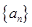 是等比数列,并写出通项公式;
是等比数列,并写出通项公式;⑵若
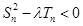 对
对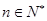 恒成立,求
恒成立,求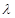 的最小值;
的最小值;⑶若
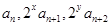 成等差数列,求正整数
成等差数列,求正整数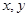 的值.
的值.(1)证明见解析,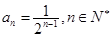 ;(2)3;(3)
;(2)3;(3)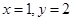
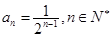 ;(2)3;(3)
;(2)3;(3)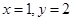
试题分析:(1)要证数列
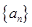 是等比数列,可根据题设求出
是等比数列,可根据题设求出 ,当然也可再求
,当然也可再求 ,虽然得出的
,虽然得出的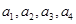 成等比数列,但前面有限项成等比不能说明所有项都成等比,必须严格证明.一般方法是把已知式
成等比数列,但前面有限项成等比不能说明所有项都成等比,必须严格证明.一般方法是把已知式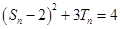 中的
中的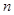 用
用 代换得到
代换得到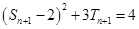 ,两式相减得
,两式相减得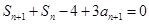 ,这个式子中把
,这个式子中把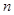 用
用 代换又得
代换又得 ,两式再相减,正好得出数列的前后项关系的递推关系
,两式再相减,正好得出数列的前后项关系的递推关系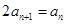 ,正是等比数列的表现.(2)由题间
,正是等比数列的表现.(2)由题间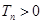 ,对不等式
,对不等式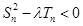 用分离参数法得
用分离参数法得 ,求
,求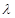 的最小值就与求
的最小值就与求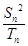 的最大值(也只要能是取值范围)联系起来了.(3)只能由
的最大值(也只要能是取值范围)联系起来了.(3)只能由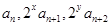 成等差数列列出唯一的等式,这个等式是关于
成等差数列列出唯一的等式,这个等式是关于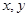 的二元方程,它属于不定方程,有无数解,只是由于
的二元方程,它属于不定方程,有无数解,只是由于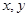 都是正整数,利用正整数的性质可得出具体的解.
都是正整数,利用正整数的性质可得出具体的解.试题解析:(1)当n=1时,
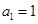 ;当n=2时,
;当n=2时,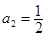
当n
 3时,有
3时,有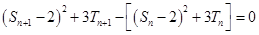 得:
得:化简得:
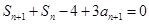 3分
3分又
 ∴
∴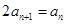
∴
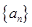 是1为首项,
是1为首项,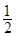 为公比的等比数列
为公比的等比数列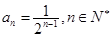 6分
6分(2)
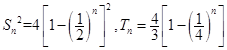
∴
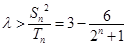 ∴
∴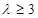 11分
11分(3)若三项成等差,则有
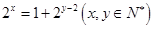
 ,右边为大于2的奇数,左边为偶数或1,不成立
,右边为大于2的奇数,左边为偶数或1,不成立∴
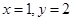 16分
16分
练习册系列答案
相关题目
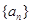 的前
的前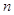 项和为
项和为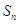 ,且
,且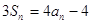 .
.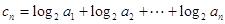 ,
,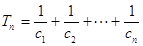 ,求使
,求使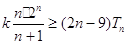 恒成立的实数
恒成立的实数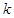 的取值范围.
的取值范围.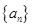 的前
的前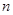 项和是
项和是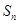 ,且
,且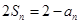 .求数列
.求数列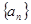 前
前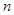 项和
项和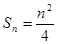 ,数列
,数列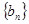 满足
满足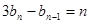 (
(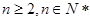 ),
),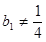 时,数列
时,数列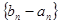 为等比数列;
为等比数列;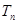 ,若数列
,若数列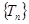 中只有
中只有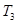 最小,求
最小,求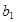 的取值范围.
的取值范围.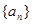 的前
的前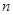 项的和
项的和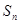 满足
满足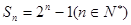 ,则数列
,则数列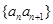 的前
的前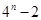
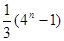
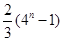
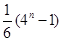
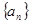 中,
中,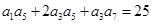 ,则
,则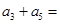 _____________.
_____________.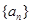 为等比数列,若
为等比数列,若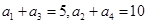 ,则公比
,则公比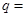 ____________.
____________.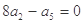 ,则
,则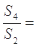 ( )
( )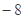
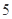
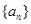 ,且
,且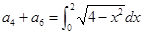 ,则
,则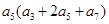 的值为( )
的值为( )