题目内容
数列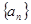 前
前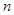 项和
项和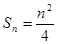 ,数列
,数列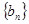 满足
满足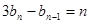 (
(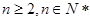 ),
),
(1)求数列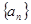 的通项公式;
的通项公式;
(2)求证:当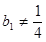 时,数列
时,数列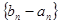 为等比数列;
为等比数列;
(3)在(2)的条件下,设数列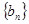 的前
的前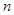 项和为
项和为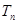 ,若数列
,若数列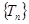 中只有
中只有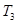 最小,求
最小,求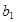 的取值范围.
的取值范围.
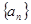 前
前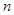 项和
项和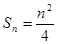 ,数列
,数列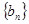 满足
满足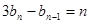 (
(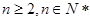 ),
),(1)求数列
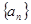 的通项公式;
的通项公式;(2)求证:当
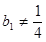 时,数列
时,数列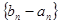 为等比数列;
为等比数列;(3)在(2)的条件下,设数列
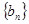 的前
的前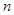 项和为
项和为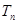 ,若数列
,若数列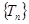 中只有
中只有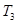 最小,求
最小,求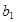 的取值范围.
的取值范围.(1)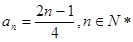 ;(2)详见解析;(3)
;(2)详见解析;(3)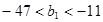 .
.
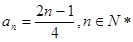 ;(2)详见解析;(3)
;(2)详见解析;(3)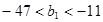 .
.试题分析:(1)由
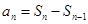 求解,注意
求解,注意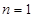 ,若满足则不用分段函数,若不满足则
,若满足则不用分段函数,若不满足则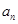 需要用分段函数表示;(2)要证明数列
需要用分段函数表示;(2)要证明数列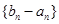 是等比数列,需要证明
是等比数列,需要证明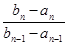 是常数,由条件只需要证明
是常数,由条件只需要证明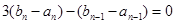 即可;(3)数列
即可;(3)数列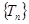 中只有
中只有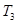 最小,可确定
最小,可确定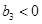 且
且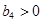 ,再证明数列
,再证明数列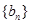 是递增数列,从而可以确定
是递增数列,从而可以确定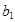 的取值范围,.
的取值范围,.试题解析:(1)

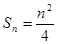 ,
,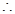
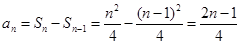 ,
,当
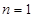 时
时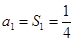 ,也满足,
,也满足,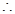
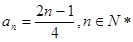 .
. (2)

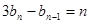 ,
,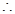
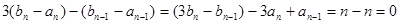 ,
,所以
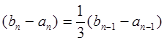 ,且
,且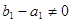 ,
,所以
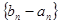 是以
是以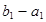 为首项、
为首项、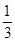 为公比的等比数列;
为公比的等比数列;(3)
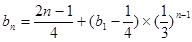 ;
;因为数列
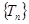 中只有
中只有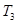 最小,所以
最小,所以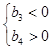 ,解得
,解得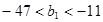 ;
;此时,
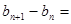
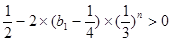 ,于是,
,于是,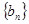 为递增数列,
为递增数列,所以
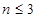 时
时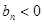 、
、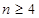 时
时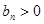 ,符合题意,综上
,符合题意,综上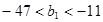 .
.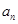 与
与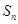 的关系,等比数列的性质,最值问题.
的关系,等比数列的性质,最值问题.
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
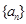 的公比为q,且
的公比为q,且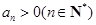 ,
,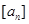 表示不超过实数
表示不超过实数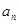 的最大整数(如
的最大整数(如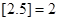 ),记
),记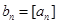 ,数列
,数列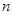 项和为
项和为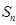 ,数列
,数列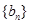 的前
的前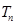 .
.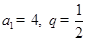 ,求
,求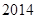 的正整数n,都有
的正整数n,都有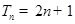 ,证明:
,证明: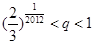 .
.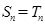 (
(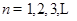 )的充分必要条件为
)的充分必要条件为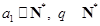 .
.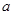 为实数,数列
为实数,数列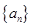 满足
满足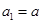 ,当
,当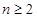 时,
时,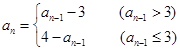 ,
, 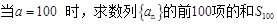 ;(5分)
;(5分)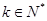 ,使
,使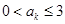 ;(5分)
;(5分)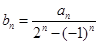 ,当
,当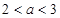 时,求证:
时,求证: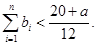 (6分)
(6分)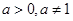 ,数列
,数列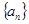 是首项为
是首项为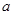 ,公比也为
,公比也为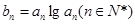
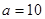 ,求数列
,求数列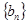 的前
的前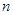 项和
项和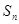 ;
;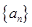 的前
的前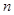 项和为
项和为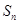 ,数列
,数列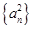 的前
的前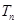 ,且
,且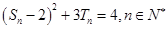 .
.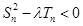 对
对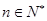 恒成立,求
恒成立,求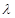 的最小值;
的最小值;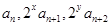 成等差数列,求正整数
成等差数列,求正整数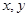 的值.
的值.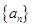 ,满足
,满足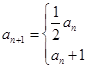
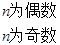 ,
,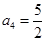 ,若
,若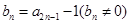 。
。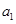 ; (2)求证:
; (2)求证: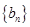 是等比数列; (3)若数列
是等比数列; (3)若数列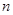 项和为
项和为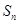 ,求
,求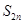
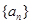 的前
的前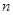 项和是
项和是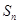 ,且
,且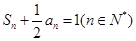 .
.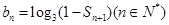 ,求适合方程
,求适合方程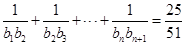 的正整数
的正整数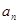 }的前n项和为
}的前n项和为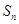 ,且
,且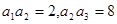 ,则
,则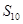 = __________.
= __________.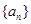 是公比为
是公比为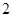 的等比数列,若
的等比数列,若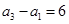 ,则
,则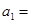 ;
; 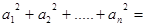 ______________.
______________.