题目内容
【题目】已知在四棱锥![]() 中,
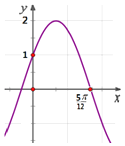
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 且平面
且平面![]() 平面
平面![]()
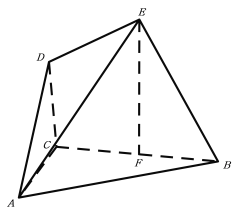
(1)设点![]() 为线段
为线段![]() 的中点,试证明
的中点,试证明![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为60°,求四棱锥
所成的角为60°,求四棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析(2)![]()
【解析】
(1)取![]() 中点为
中点为![]() ,通过面面垂直,结合
,通过面面垂直,结合![]() //
//![]() ,即可容易证明;
,即可容易证明;
(2)根据线面角,求得![]() ,先证
,先证![]() 平面
平面![]() ,结合
,结合![]() 即可容易求得.
即可容易求得.
(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() 和
和![]() ,
,

∵在![]() 中
中![]() ,∴
,∴![]() .
.
由于平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,∴
,∴![]() 平面
平面![]() .
.
又∵![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,∴
的中点,∴![]() //
//![]() 且
且![]() .
.
又![]() //
//![]() ,
,![]() ,∴
,∴![]() //
//![]() 且
且![]() .
.
∴四边形![]() 为平行四边形.∴
为平行四边形.∴![]() //
//![]() ,
,
∴![]() 平面
平面![]() .
.
(2)由(1)中所证,不妨取![]() 中点为
中点为![]() ,则一定有
,则一定有![]() 平面
平面![]() .
.
所以直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
由于![]() ,∴
,∴![]() ,
,
又![]() //
//![]() ∴
∴![]() 、
、![]() 点到平面
点到平面![]() 的距离相等,
的距离相等,
∵平面![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ∴
∴![]() 点到平面
点到平面![]() 的距离等于2.
的距离等于2.
故可得![]() ;
;
![]() .
.
又因为![]() 点到平面
点到平面![]() 的距离为
的距离为![]() ,
,![]() 点到平面
点到平面![]() 的距离为
的距离为![]() ,
,
∴![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目