题目内容
已知函数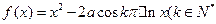 ,
,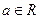 且
且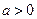 ).
).
(1)讨论函数f(x)的单调性;
(2)若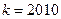 ,方程f (x) ="2" a x有惟一解时,求
,方程f (x) ="2" a x有惟一解时,求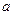 的值。
的值。
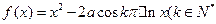 ,
,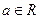 且
且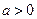 ).
).(1)讨论函数f(x)的单调性;
(2)若
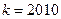 ,方程f (x) ="2" a x有惟一解时,求
,方程f (x) ="2" a x有惟一解时,求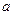 的值。
的值。(1)当k是奇数时,f(x)在(0,+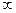 )上是增函数 ;当k是偶数时,f(x)在
)上是增函数 ;当k是偶数时,f(x)在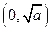 是减函数,在
是减函数,在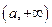 是增函数 (2)
是增函数 (2)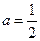
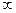 )上是增函数 ;当k是偶数时,f(x)在
)上是增函数 ;当k是偶数时,f(x)在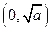 是减函数,在
是减函数,在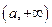 是增函数 (2)
是增函数 (2)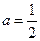
(1)由已知得,x>0且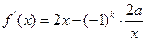 .
.
当k是奇数时,则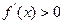 ,则f(x)在(0,+
,则f(x)在(0,+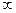 )上是增函数; ……(2分)
)上是增函数; ……(2分)
当k是偶数时,则,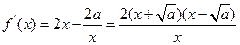 , ……(3分)
, ……(3分)
所以当x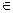
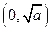 时,
时,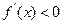 , 当x
, 当x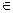
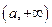 时,
时,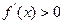 ,
,
故当k是偶数时,f(x)在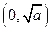 是减函数,在
是减函数,在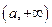 是增函数.……(5分)
是增函数.……(5分)
(Ⅱ)若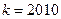 ,则
,则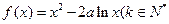 )
)
记g (x) = f (x) – 2ax = x2 – 2 a xlnx – 2ax,
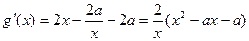 ,
,
若方程f(x)=2ax有唯一解,即g(x)=0有唯一解;……(6分)
令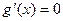 ,得
,得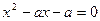 ,
,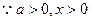
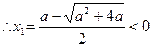 (舍去)
(舍去)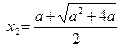 ……(7分)
……(7分)
当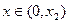 时,
时,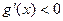 ,
,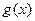 在
在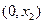 是单调递减函数;
是单调递减函数;
当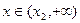 时,
时,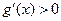 ,
,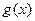 在
在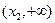 上是单调递增函数。
上是单调递增函数。
当x=x2时,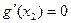 ,
,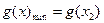 …………(8分)
…………(8分)
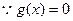 有唯一解,
有唯一解,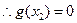
则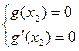 ,即
,即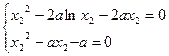 ………(9分)
………(9分)
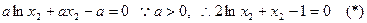 …………(10分)
…………(10分)
设函数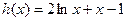 ,
,
∵在x>0时, h (x)是增函数,∴h (x) = 0至多有一解。
∵h (1) =" 0," ∴方程(*)的解为x2 = 1,即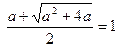 ,解得
,解得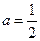 。…………(12分)
。…………(12分)
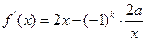 .
.当k是奇数时,则
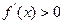 ,则f(x)在(0,+
,则f(x)在(0,+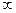 )上是增函数; ……(2分)
)上是增函数; ……(2分)当k是偶数时,则,
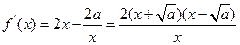 , ……(3分)
, ……(3分)所以当x
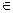
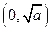 时,
时,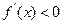 , 当x
, 当x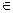
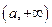 时,
时,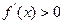 ,
, 故当k是偶数时,f(x)在
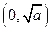 是减函数,在
是减函数,在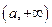 是增函数.……(5分)
是增函数.……(5分)(Ⅱ)若
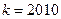 ,则
,则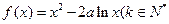 )
)记g (x) = f (x) – 2ax = x2 – 2 a xlnx – 2ax,
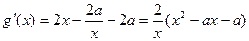 ,
,若方程f(x)=2ax有唯一解,即g(x)=0有唯一解;……(6分)
令
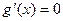 ,得
,得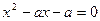 ,
,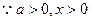
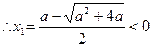 (舍去)
(舍去)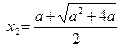 ……(7分)
……(7分)当
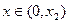 时,
时,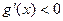 ,
,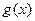 在
在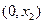 是单调递减函数;
是单调递减函数;当
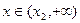 时,
时,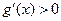 ,
,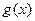 在
在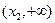 上是单调递增函数。
上是单调递增函数。当x=x2时,
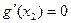 ,
,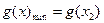 …………(8分)
…………(8分)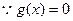 有唯一解,
有唯一解,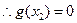
则
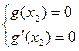 ,即
,即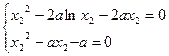 ………(9分)
………(9分)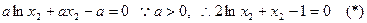 …………(10分)
…………(10分)设函数
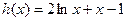 ,
,∵在x>0时, h (x)是增函数,∴h (x) = 0至多有一解。
∵h (1) =" 0," ∴方程(*)的解为x2 = 1,即
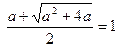 ,解得
,解得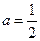 。…………(12分)
。…………(12分)
练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
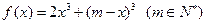 .
.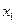 、
、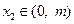 ,求证:①
,求证:①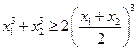 ;
;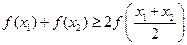 .
.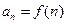 ,
,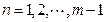 ,其中
,其中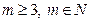 ,求证:
,求证: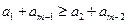 ;
;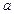 、
、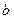 、
、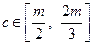 ,问:以
,问:以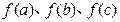 的值为长的三条线段是否可构成三角形?请说明理由.
的值为长的三条线段是否可构成三角形?请说明理由.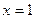 是函数
是函数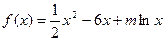 的一个极值点。
的一个极值点。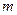 ;
;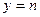 与函数
与函数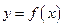 的图象有3个交点,求
的图象有3个交点,求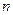 的取值范围;
的取值范围;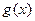 =(
=(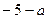 )
)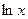 +
+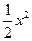 +(6-
+(6-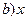 +2(
+2(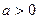 ),
),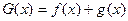 ,若
,若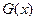 =0有两个零点
=0有两个零点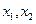 ,且
,且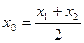 ,试探究
,试探究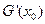 值的符号
值的符号
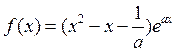 (
(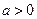 )
)
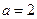 时,求函数
时,求函数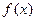 的单调区间;
的单调区间;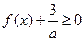 对
对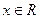 恒成立,求a的取值范围
恒成立,求a的取值范围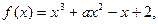
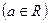
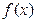 在
在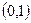 上是减函数,求
上是减函数,求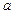 的最大值;
的最大值;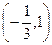 ,求函数y=
,求函数y=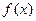 图像过点
图像过点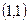 的切线与两坐标轴围成图形的面积。
的切线与两坐标轴围成图形的面积。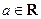 ,函数
,函数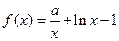 ,
,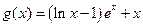 (其中
(其中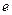 为自然对数的底数).
为自然对数的底数).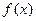 在区间
在区间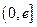 上的最小值;
上的最小值;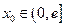 ,使曲线
,使曲线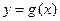 在点
在点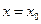 处的切线与
处的切线与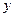 轴垂直? 若存在,求出
轴垂直? 若存在,求出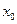 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.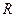 上的函数
上的函数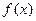 满足
满足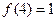 ,
,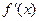 为
为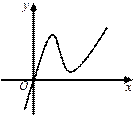
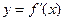 的图像如右图所示,
的图像如右图所示,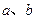 满足
满足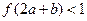 ,则
,则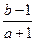 的取值范围是 .
的取值范围是 .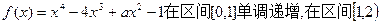 单调递减,
单调递减,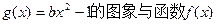 的图象恰有3个交点,若
的图象恰有3个交点,若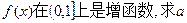 的取值范围数b的值;若不存在,试说明理由。
的取值范围数b的值;若不存在,试说明理由。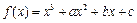 在
在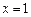 和
和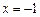 时取极值,且
时取极值,且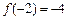 .
.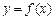 的表达式;
的表达式;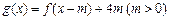 在区间
在区间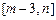 上的值域为
上的值域为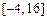 ,试求
,试求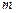 、n应满足的条件。
、n应满足的条件。