题目内容
(本小题满分14分)已知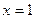 是函数
是函数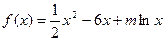 的一个极值点。
的一个极值点。
(Ⅰ)求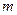 ;
;
(Ⅱ)若直线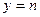 与函数
与函数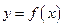 的图象有3个交点,求
的图象有3个交点,求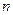 的取值范围;
的取值范围;
(Ⅲ)设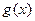 =(
=(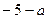 )
)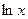 +
+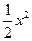 +(6-
+(6-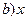 +2(
+2(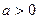 ),
),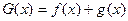 ,若
,若
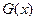 =0有两个零点
=0有两个零点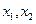 ,且
,且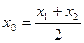 ,试探究
,试探究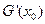 值的符号
值的符号
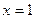 是函数
是函数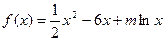 的一个极值点。
的一个极值点。(Ⅰ)求
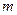 ;
;(Ⅱ)若直线
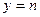 与函数
与函数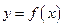 的图象有3个交点,求
的图象有3个交点,求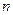 的取值范围;
的取值范围;(Ⅲ)设
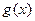 =(
=(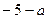 )
)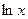 +
+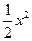 +(6-
+(6-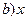 +2(
+2(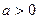 ),
),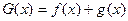 ,若
,若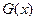 =0有两个零点
=0有两个零点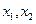 ,且
,且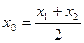 ,试探究
,试探究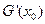 值的符号
值的符号
(Ⅰ)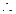
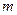 =5
=5
(Ⅱ)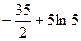 <
<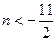
(Ⅲ)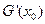 的符号为正
的符号为正
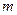 =5
=5(Ⅱ)
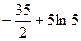 <
<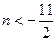
(Ⅲ)
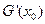 的符号为正
的符号为正本题主要考查函数、导数、不等式等基础知识,考查推理论证能力、运算求解能力,考查
数形结合思想、化归与转化思想、分类与整合思想。
 (Ⅰ)因为
(Ⅰ)因为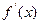 =
=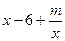
所以 =0,
=0,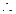
 =5-----
=5----- -------------------------------3分
-------------------------------3分
(Ⅱ)由(Ⅰ)知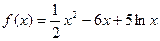 (
(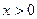 )
)
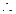
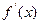 =
=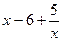 =
= =
=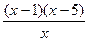 ------------------------5分
------------------------5分
当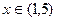 时,
时,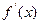 <0,
<0,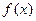 单调递减;
单调递减;
当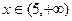 或
或 时,
时,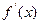 >0,
>0,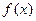 单调递增.
单调递增.
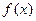 的极大值为
的极大值为 =
=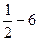 =
=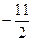 ,
,
极小值为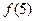 =
=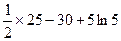 =
=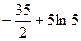 ,
,
又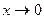 时,
时,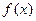
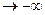 ,
,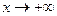 时,
时,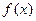
 -----------------7分
-----------------7分
结合图像可知:当且仅当 时
时
直线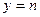 与函数
与函数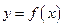 的图象有3个交点
的图象有3个交点
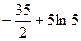 <
<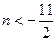 ------------------------------------9分
------------------------------------9分
(III)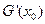 的符号为正. 证明如下:
的符号为正. 证明如下:
因为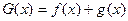 =
= +(
+(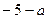 )
)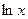 +
+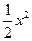 +(6-
+(6-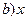 +2
+2
=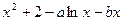 有两个零点
有两个零点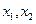 ,则有
,则有
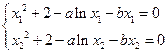 ,
,
两式相减得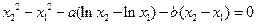
即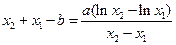 ,
,
于是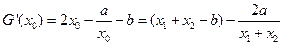
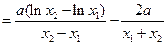
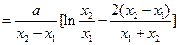
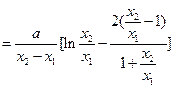 -------------------------11分
-------------------------11分
①当
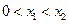 时,令
时,令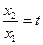 ,则
,则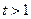 ,且
,且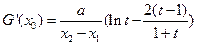 .
.
设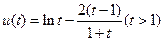 ,
,
则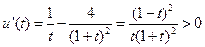 ,
,
则 在
在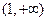 上为增函数.而
上为增函数.而
 ,所以
,所以 ,
,
即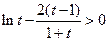 . 又因为
. 又因为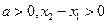 ,所以
,所以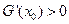 . ------12分
. ------12分
②当 时,同理可得:
时,同理可得: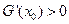 . --------------------------13分
. --------------------------13分
综上所述: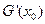 的符号为正------------------------------------14分
的符号为正------------------------------------14分
数形结合思想、化归与转化思想、分类与整合思想。
 (Ⅰ)因为
(Ⅰ)因为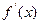 =
=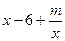
所以
 =0,
=0,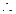
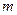 =5-----
=5----- -------------------------------3分
-------------------------------3分(Ⅱ)由(Ⅰ)知
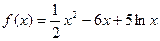 (
(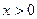 )
)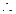
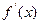 =
=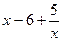 =
= =
=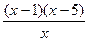 ------------------------5分
------------------------5分当
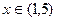 时,
时,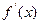 <0,
<0,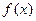 单调递减;
单调递减;当
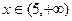 或
或 时,
时,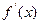 >0,
>0,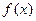 单调递增.
单调递增.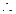
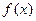 的极大值为
的极大值为 =
=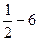 =
=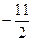 ,
,极小值为
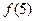 =
=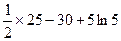 =
=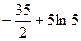 ,
,又
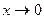 时,
时,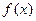
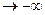 ,
,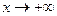 时,
时,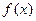
 -----------------7分
-----------------7分结合图像可知:当且仅当
 时
时直线
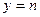 与函数
与函数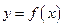 的图象有3个交点
的图象有3个交点
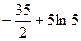 <
<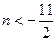 ------------------------------------9分
------------------------------------9分(III)
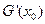 的符号为正. 证明如下:
的符号为正. 证明如下:因为
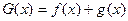 =
= +(
+(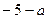 )
)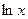 +
+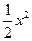 +(6-
+(6-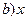 +2
+2=
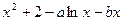 有两个零点
有两个零点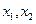 ,则有
,则有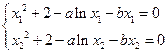 ,
,两式相减得
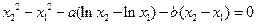
即
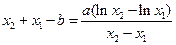 ,
,于是
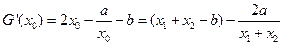
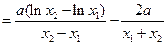
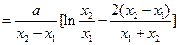
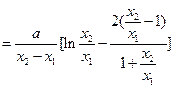 -------------------------11分
-------------------------11分①当

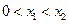 时,令
时,令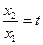 ,则
,则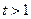 ,且
,且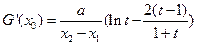 .
.设
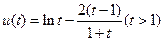 ,
,则
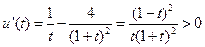 ,
,则
 在
在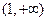 上为增函数.而
上为增函数.而
 ,所以
,所以 ,
,即
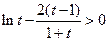 . 又因为
. 又因为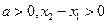 ,所以
,所以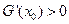 . ------12分
. ------12分②当
 时,同理可得:
时,同理可得: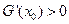 . --------------------------13分
. --------------------------13分综上所述:
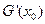 的符号为正------------------------------------14分
的符号为正------------------------------------14分
练习册系列答案
相关题目
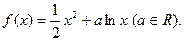
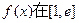 上
上 是增函数,求
是增函数,求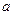 的取值范围;
的取值范围;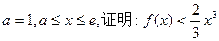 ;
; 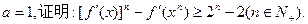
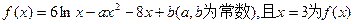 的一个极值点.
的一个极值点.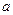 ;
;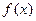 的单调区间;
的单调区间;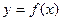 的图象与x轴有且只有3个交点,求b的取值范围.
的图象与x轴有且只有3个交点,求b的取值范围.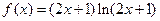 .
.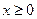 ,都有
,都有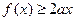 成立,求实数a的取值范围.
成立,求实数a的取值范围.
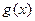 的单调递增区间;
的单调递增区间;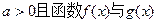 的图像有公共点,且在该点处的切线相同,用a表示b,并求b的最大值。
的图像有公共点,且在该点处的切线相同,用a表示b,并求b的最大值。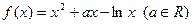
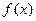 在
在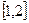 上是减函数,求实数
上是减函数,求实数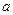 的取值范围;
的取值范围;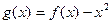 ,是否存在实数
,是否存在实数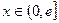 时,函数
时,函数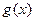 的最小值是
的最小值是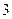 ?若存在,求出实数
?若存在,求出实数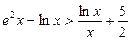 .
.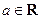 ,函数
,函数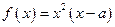 .
.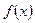 在区间
在区间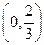 内是减函数,求实数
内是减函数,求实数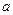 的取值范围;
的取值范围;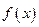 在区间
在区间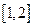 上的最小值
上的最小值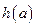 ;
;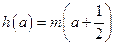 有两个不相等的实数解,求实数
有两个不相等的实数解,求实数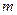 的取值范围.
的取值范围.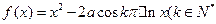 ,
,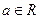 且
且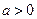 ).
).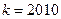 ,方程f (x) ="2" a x有惟一解时,求
,方程f (x) ="2" a x有惟一解时,求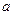 的值。
的值。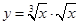 的导数
的导数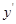 为( ).
为( ).


