题目内容
【题目】如图,PA⊥圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E、F分别是点A在PB、PC上的射影,给出下列结论: ①AF⊥PB;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC;⑤平面PBC⊥平面PAC.其中正确命题的序号是 . 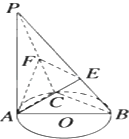
【答案】①②③⑤
【解析】解:∵PA⊥圆O所在的平面α,BCα,∴PA⊥BC, AB是圆O的直径,C是圆O上的一点,∴BC⊥AC,
又PA∩AC=A,∴BC⊥平面PAC,AF平面PAC,
∴BC⊥AF,又AF⊥PC,PC∩BC=C,
∴AF⊥平面PBC,PB平面PBC,
∴AF⊥PB,即①正确;
又AE⊥PB,同理可证PB⊥平面AFE,EF平面AFE,
∴EF⊥PB,即②正确;
由BC⊥平面PAC,AF平面PAC知,BC⊥AF,即③正确;
∵AF⊥平面PBC(前边已证),AE∩AF=A,
∴AE不与平面PBC垂直,故④错误,
∵AF⊥平面PBC,且AF平面PAC,
∴平面PAC⊥平面PBC,即⑤正确.
综上所述,正确结论的序号是①②③⑤.
所以答案是:①②③⑤
【考点精析】解答此题的关键在于理解空间中直线与平面之间的位置关系的相关知识,掌握直线在平面内—有无数个公共点;直线与平面相交—有且只有一个公共点;直线在平面平行—没有公共点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目