ƒøƒ⁄»ð
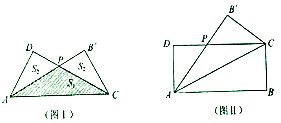
°æƒø°ø∂®“£∫f1£®x£©=f£®x£©£¨µ±n°ð2«“x° N* ±£¨fn£®x£©=f£®fn©Å1£®x£©£©£¨∂‘”⁄∫Ø ˝f£®x£©∂®“”ڃ⁄µƒx0 £¨ »Ù’˝‘⁄’˝’˚ ˝n « πµ√fn£®x0£©=x0≥…¡¢µƒ◊Ó–°’˝’˚ ˝£¨‘Ú≥∆n «µ„x0µƒ◊Ó–°’˝÷Ð∆⁄£¨x0≥∆Œ™f£®x£©µƒn°´÷Ð∆⁄µ„£¨“—÷™∂®“‘⁄[0£¨1]…œµƒ∫Ø ˝f£®x£©µƒÕºœÛ»ÁÕº£¨∂‘”⁄∫Ø ˝f£®x£©£¨œ¬¡–Àµ∑®’˝»∑µƒ «£®–¥≥ˆÀ˘”–’˝»∑√¸Ã‚µƒ±ý∫≈£©
¢Ÿ1 «f£®x£©µƒ“ª∏ˆ3°´÷Ð∆⁄µ„£ª
¢⁄3 «µ„ ![]() µƒ◊Ó–°’˝÷Ð∆⁄£ª
µƒ◊Ó–°’˝÷Ð∆⁄£ª
¢€∂‘”⁄»Œ“‚’˝’˚ ˝n£¨∂º”–fn£® ![]() £©=
£©= ![]() £ª
£ª
¢Ð»Ùx0° £® ![]() £¨1]£¨‘Úx0 «f£®x£©µƒ“ª∏ˆ2°´÷Ð∆⁄µ„£Æ
£¨1]£¨‘Úx0 «f£®x£©µƒ“ª∏ˆ2°´÷Ð∆⁄µ„£Æ
°æ¥∞∏°ø¢Ÿ¢⁄¢€
°æΩ‚Œˆ°øΩ‚£∫f1£®1£©=f£®1£©=0£¨f2£®1£©=f£®f1£®1£©£©=f£®0£©= ![]() £¨f3£®1£©=f£®f2£®1£©£©=f£®
£¨f3£®1£©=f£®f2£®1£©£©=f£® ![]() £©=1£¨π ¢Ÿ1 «f£®x£©µƒ“ª∏ˆ3°´÷Ð∆⁄µ„£¨’˝»∑£ª
£©=1£¨π ¢Ÿ1 «f£®x£©µƒ“ª∏ˆ3°´÷Ð∆⁄µ„£¨’˝»∑£ª
f1£® ![]() £©=f£®
£©=f£® ![]() £©=1£¨f2£®
£©=1£¨f2£® ![]() £©=f£®f1£®
£©=f£®f1£® ![]() £©£©=f£®1£©=0£¨f3£®
£©£©=f£®1£©=0£¨f3£® ![]() £©=f£®f2£®
£©=f£®f2£® ![]() £©£©=f£®0£©=
£©£©=f£®0£©= ![]() £¨
£¨
π ¢⁄3 «µ„ ![]() µƒ◊Ó–°’˝÷Ð∆⁄£¨’˝»∑£ª
µƒ◊Ó–°’˝÷Ð∆⁄£¨’˝»∑£ª
”…“—÷™÷–µƒÕºœÛø…µ√£∫f£® ![]() £©=
£©= ![]() £¨
£¨
π f1£® ![]() £©=f£®
£©=f£® ![]() £©=
£©= ![]() £¨f2£®
£¨f2£® ![]() £©=f£®f1£®
£©=f£®f1£® ![]() £©£©=f£®
£©£©=f£® ![]() £©=
£©= ![]() £¨f3£®
£¨f3£® ![]() £©=f£®f2£®
£©=f£®f2£® ![]() £©£©=f£®
£©£©=f£® ![]() £©=
£©= ![]() £¨
£¨
π ¢€∂‘”⁄»Œ“‚’˝’˚ ˝n£¨∂º”–fn£® ![]() £©=
£©= ![]() £¨’˝»∑£ª
£¨’˝»∑£ª
¢Ð»Ùx0=1£¨‘Úx0° £® ![]() £¨1]£¨µ´x0 «f£®x£©µƒ“ª∏ˆ3°´÷Ð∆⁄µ„£¨π ¥ÌŒÛ£Æ
£¨1]£¨µ´x0 «f£®x£©µƒ“ª∏ˆ3°´÷Ð∆⁄µ„£¨π ¥ÌŒÛ£Æ
À˘“‘¥∞∏ «£∫¢Ÿ¢⁄¢€
°æøºµ„æ´Œˆ°ø±æÂ÷˜“™øº≤È¡À√¸Ã‚µƒ’ʺŸ≈–∂œ”Δ¶”√µƒœýπÿ÷™ ∂µ„£¨–Ë“™’∆Œ’¡Ω∏ˆ√¸Ã‚ª•Œ™ƒÊ∑Ò√¸Ã‚£¨À¸√«”–œýÕ¨µƒ’ʺŸ–‘£ª¡Ω∏ˆ√¸Ã‚Œ™ª•ƒÊ√¸Ã‚ªÚª•∑Ò√¸Ã‚£¨À¸√«µƒ’ʺŸ–‘√ª”–πÿœµ≤≈ƒÐ’˝»∑Ω‚¥¥À£Æ

 ≤π≥‰œ∞ÂΩ≠À’œµ¡–¥∞∏
≤π≥‰œ∞ÂΩ≠À’œµ¡–¥∞∏ —ß¡∑øÏ≥µµ¿ø⁄À„–ƒÀ„ÀŸÀ„ÃÏÃÏ¡∑œµ¡–¥∞∏
—ß¡∑øÏ≥µµ¿ø⁄À„–ƒÀ„ÀŸÀ„ÃÏÃÏ¡∑œµ¡–¥∞∏°æƒø°ø‘⁄∏þ÷–—ßœ∞π˝≥Ã÷–£¨Õ¨—ß√«æ≠≥£’‚—˘Àµ£∫°∞ ˝—ߌԿÌ≤ª∑÷º“£¨»Áπ˚ŒÔ¿Ì≥…º®∫√£¨ƒ«√¥—ßœ∞ ˝—ßæÕ√ª ≤√¥Œ £ư±ƒ≥∞ý’Î∂‘°∞∏þ÷–…˙ŒÔ¿Ì—ßœ∞∂‘ ˝—ß—ßœ∞µƒ”∞œÏ°±Ω¯––—–æø£¨µ√µΩ¡ÀÀ’∂Ì…˙µƒŒÔ¿Ì≥…º®”Î ˝—ß≥…º®æþ”–œþ–‘œýπÿπÿœµµƒΩ·¬€£Æœ÷¥”∏√∞ýÀʪ˙≥È»°5√˚—ß…˙‘⁄“ª¥Œøº ‘÷–µƒ ˝—ß∫ՌԿÌ≥…º®£¨»Á±Ì£∫
≥…º® ±ý∫≈ | 1 | 2 | 3 | 4 | 5 |
ŒÔ¿Ì£®x£© | 90 | 85 | 74 | 68 | 63 |
˝—ߣ®y£© | 130 | 125 | 110 | 95 | 90 |
£®1£©«Û ˝—ß≥…º®y∂‘ŒÔ¿Ì≥…º®xµƒœþ–‘ªÿπÈ∑Ω≥à ![]() =
= ![]() x+
x+ ![]() £®
£® ![]() æ´»∑µΩ0.1£©£Æ»Ùƒ≥Œª—ß…˙µƒŒÔ¿Ì≥…º®Œ™80∑÷£¨‘§≤‚À˚µƒ ˝—ß≥…º®£ª
æ´»∑µΩ0.1£©£Æ»Ùƒ≥Œª—ß…˙µƒŒÔ¿Ì≥…º®Œ™80∑÷£¨‘§≤‚À˚µƒ ˝—ß≥…º®£ª
£®2£©“™¥”≥È»°µƒ’‚ŒÂŒª—ß…˙÷–Àʪ˙—°≥ˆ2Œª≤Œº”“ªœÓ÷™ ∂æ∫»¸£¨«Û—°÷–µƒ—ß…˙µƒ ˝—ß≥…º®÷¡…Ÿ”–“ªŒª∏þ”⁄120∑÷µƒ∏≈¬ £Æ£®≤Œøºπ´ Ω£∫ ![]() =
= 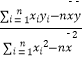 £¨
£¨ ![]() =
= ![]() ©Å
©Å ![]() £© £®≤Œøº ˝æð£∫902+852+742+682+632=29394£¨90°¡°¡125+74°¡110+68°¡95+63°¡90=42595£©
£© £®≤Œøº ˝æð£∫902+852+742+682+632=29394£¨90°¡°¡125+74°¡110+68°¡95+63°¡90=42595£©