题目内容
12.棱长为1的正方体ABCD-A1B1C1D1的8个顶点都在球O的表面上,E,F分别为棱AB,A1D1的中点,则经过E,F球的截面面积的最小值为( )| A. | $\frac{3}{8}$π | B. | $\frac{π}{2}$ | C. | $\frac{5}{8}$π | D. | $\frac{7}{8}$π |
分析 先求球的半径,再求EF,球心到截面圆的距离,OP,然后求出截面圆的半径,就是图中QP即可得出结论.
解答 解:因为正方体内接于球,所以2R=$\sqrt{{1}^{2}+{1}^{2}+{1}^{1}}$=$\sqrt{3}$,R=$\frac{\sqrt{3}}{2}$,
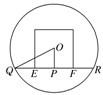
过球心O和点E、F的大圆的截面图如图所示,
则直线被球截得的线段为QR,过点O作OP⊥QR,垂足为点P,EF=$\frac{\sqrt{6}}{2}$,OF=$\frac{\sqrt{2}}{2}$
OP=$\sqrt{(\frac{\sqrt{2}}{2})^{2}-(\frac{\sqrt{6}}{4})^{2}}$=$\frac{\sqrt{2}}{4}$,
所以,在△QPO中,QP=$\sqrt{(\frac{\sqrt{3}}{2})^{2}-(\frac{\sqrt{2}}{4})^{2}}$=$\frac{\sqrt{10}}{4}$.
所以所求经过E、F的平面截球O所得的截面的面积的最小值是:$π•(\frac{\sqrt{10}}{4})^{2}$=$\frac{5}{8}π$.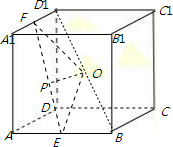
故选:C.
点评 本题考查组合体的结构特征,球的内接多面体,截面圆的面积,考查空间想象能力,计算能力,是中档题.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
20.若sinα=$\frac{3}{5}$,且α是第二象限角,则tanα=( )
| A. | -$\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $±\frac{4}{3}$ | D. | $±\frac{3}{4}$ |
17.方程x2-4y2+3x-6y=0表示的图形是( )
| A. | 一条直线 | B. | 两条直线 | C. | 一个圆 | D. | 以上答案都不对 |
2.已知角α的终边上一点P(-3,4),则cosα的值为( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $-\frac{3}{5}$ |
