题目内容
(本题满分14分)已知函数
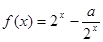 (
(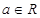 ),将
),将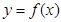 的图象向右平移两个单位,得到函数
的图象向右平移两个单位,得到函数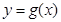 的图象,函数
的图象,函数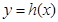 与函数
与函数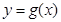 的图象关于直线
的图象关于直线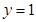 对称.
对称.(1)求函数
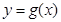 和
和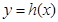 的解析式;
的解析式;(2)若方程
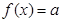 在
在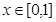 上有且仅有一个实根,求
上有且仅有一个实根,求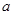 的取值范围;
的取值范围;(3)设
 ,已知
,已知 对任意的
对任意的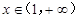 恒成立,求
恒成立,求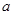 的取值范围.
的取值范围.解:(1)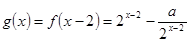 , ……1分
, ……1分
设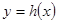 的图像上一点
的图像上一点 ,点
,点 关于
关于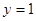 的对称点为
的对称点为 ,……2分
,……2分
由点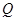 在
在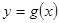 的图像上,所以
的图像上,所以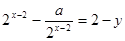 ,
,
于是 即
即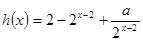 . ……4分
. ……4分
(2)设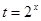 ,
,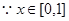 ,
,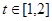
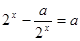 得
得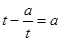 ,即
,即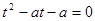 在
在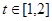 上有且仅有一个实根 ……5分
上有且仅有一个实根 ……5分
设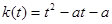 ,对称轴
,对称轴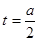
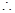
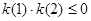 ① ……6分 或
① ……6分 或 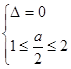 ② ……7分
② ……7分
由①得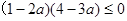 ,即
,即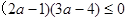 ,
,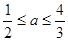 ……8分
……8分
由②得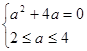 无解
无解
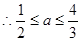 ……9分
……9分
(3)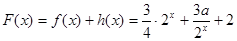
由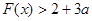 ,化简得
,化简得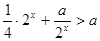 ,设
,设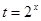 ,
,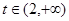
即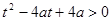 对任意
对任意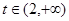 恒成立. ……10分
恒成立. ……10分
解法一:设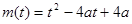 ,对称轴
,对称轴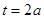
则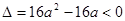 ③ ……11分 或
③ ……11分 或 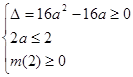 ④ ……12分
④ ……12分
由③得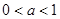 , 由④得
, 由④得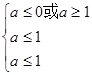 ,即
,即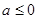 或
或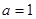
综上,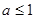 . ……14分
. ……14分
解法二:注意到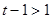 ,分离参数得
,分离参数得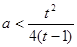 对任意
对任意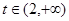 恒成立 ……11分
恒成立 ……11分
设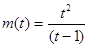 ,
,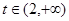 ,即
,即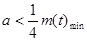
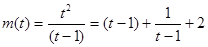 ……12分
……12分
可证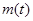 在
在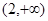 上单调递增 ……13分
上单调递增 ……13分
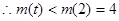
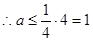 ……14分
……14分
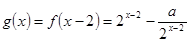 , ……1分
, ……1分设
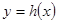 的图像上一点
的图像上一点 ,点
,点 关于
关于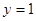 的对称点为
的对称点为 ,……2分
,……2分由点
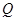 在
在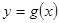 的图像上,所以
的图像上,所以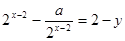 ,
,于是
 即
即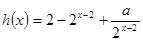 . ……4分
. ……4分(2)设
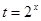 ,
,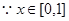 ,
,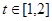
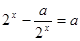 得
得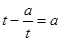 ,即
,即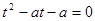 在
在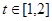 上有且仅有一个实根 ……5分
上有且仅有一个实根 ……5分设
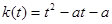 ,对称轴
,对称轴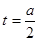
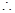
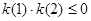 ① ……6分 或
① ……6分 或 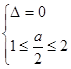 ② ……7分
② ……7分由①得
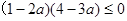 ,即
,即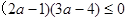 ,
,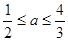 ……8分
……8分由②得
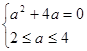 无解
无解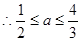 ……9分
……9分(3)
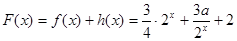
由
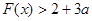 ,化简得
,化简得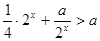 ,设
,设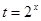 ,
,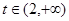
即
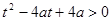 对任意
对任意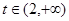 恒成立. ……10分
恒成立. ……10分解法一:设
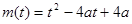 ,对称轴
,对称轴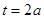
则
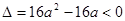 ③ ……11分 或
③ ……11分 或 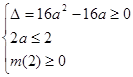 ④ ……12分
④ ……12分由③得
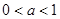 , 由④得
, 由④得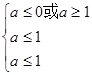 ,即
,即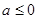 或
或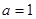
综上,
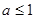 . ……14分
. ……14分解法二:注意到
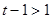 ,分离参数得
,分离参数得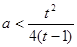 对任意
对任意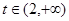 恒成立 ……11分
恒成立 ……11分设
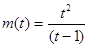 ,
,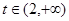 ,即
,即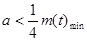
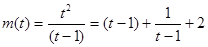 ……12分
……12分可证
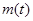 在
在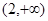 上单调递增 ……13分
上单调递增 ……13分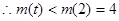
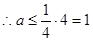 ……14分
……14分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
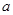 值如何变化,函数
值如何变化,函数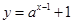 (
(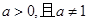 )恒过定点( )
)恒过定点( )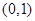
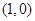
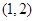
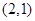
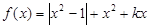 ,且定义域为(0,2).
,且定义域为(0,2).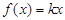 +3在(0,2)上的解;
+3在(0,2)上的解;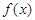 是定义域(0,2)上的单调函数,求实数
是定义域(0,2)上的单调函数,求实数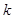 的取值范围;
的取值范围;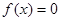 在(0,2)上有两个不同的解
在(0,2)上有两个不同的解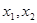 ,求k的取值范围。
,求k的取值范围。 的方程
的方程 在
在 没有实数根,则
没有实数根,则 的取值范围是
的取值范围是
 与直线
与直线 有两个交点时,实数
有两个交点时,实数 的取值范围是
的取值范围是
 与点
与点 在直线
在直线 两侧, 则3b-2a>1;
两侧, 则3b-2a>1; 的图像向右平移
的图像向右平移 个单位后变为偶函数,则
个单位后变为偶函数,则 的最小值是
的最小值是 ;其中正确的结论是:__________________
;其中正确的结论是:__________________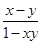 );当x∈(-1,0)时,有f(x)>0.若p=f(
);当x∈(-1,0)时,有f(x)>0.若p=f(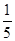 )+f(
)+f(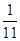 ),Q=f(
),Q=f(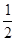 ),R=f(0);则 P,Q,R的大小关系为
),R=f(0);则 P,Q,R的大小关系为 可以产生区间[0,1]上的均匀随机数,若
可以产生区间[0,1]上的均匀随机数,若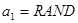 ,
,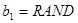 且
且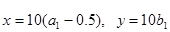 ,
,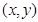 为点
为点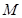 的坐标,则点
的坐标,则点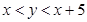 的概率是 .
的概率是 .  销活动,当该商品的售价为
销活动,当该商品的售价为 元时,全年的促销费用为
元时,全年的促销费用为 万元;根据以往的销售经验,实施促销后的年销售量
万元;根据以往的销售经验,实施促销后的年销售量 万件,其中4
万件,其中4 为常数.当该商品的售价为6元时,年销售量为49万件.
为常数.当该商品的售价为6元时,年销售量为49万件. 的值;
的值; 万元与售价
万元与售价 ,
, ,
, ,则由表中数据确定
,则由表中数据确定 、
、 、
、 依次对应 ( ).
依次对应 ( ). 、
、 、
、
