题目内容
如图,在四棱锥P—ABCD中,PA⊥底面ABCD,∠![]() , AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.
, AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.
(Ⅰ)证明:CD⊥平面BEF;
(Ⅱ)设![]() ,
,
求k的值.

(Ⅰ)证明见解析(Ⅱ)![]()
解析:
(Ⅰ)证明:  .………………………2分
.………………………2分
PA⊥平面ABCD,AD⊥CD. ……………………………………………3分
![]()
 . ………………………………………5分
. ………………………………………5分
∴ CD⊥平面BEF. ……………………………………………………………………6分
(Ⅱ)连结AC且交BF于H,可知H是AC中点,连结EH,
由E是PC中点,得EH∥PA, PA⊥平面ABCD.
得EH⊥平面ABCD,且EH![]() .…………………………………………8分
.…………………………………………8分
作HM⊥BD于M,连结EM,由三垂线定理可得EM⊥BD.
故∠EMH为二面角E—BD—F的平面角,故∠EMH=600.……………………10分
∵ Rt△HBM∽Rt△DBF,
 故
故![]() .
.
得![]() , 得
, 得 ![]() .
.
在Rt△EHM中,![]()
 得
得 ![]() ………………………………………………………12分
………………………………………………………12分
解法2:(Ⅰ)证明,以A为原点,
建立如图空间直角坐标系![]() .
.
则![]() ,
,![]() ,
,![]()
设PA = k,则![]() ,
,
![]() ,
,![]() .………………………………………………………2分
.………………………………………………………2分
得![]()
![]() .…………………………4分
.…………………………4分
有 ………………6分
………………6分
(Ⅱ)![]() …7分
…7分 ![]() .
.
设平面BDE的一个法向量![]() ,
,
则 得
得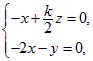 取
取![]() ……………10分 由
……………10分 由 
![]() ………………………………………11分
………………………………………11分
得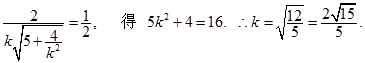 …………………12分
…………………12分

练习册系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a,
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a, 如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点
如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点 (2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.
(2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.