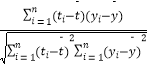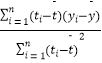题目内容
【题目】已知椭圆 ![]() =1(a>b>0)的左右焦点F1、F2 , 离心率为
=1(a>b>0)的左右焦点F1、F2 , 离心率为 ![]() ,双曲线方程为
,双曲线方程为 ![]() =1(a>0,b>0),直线x=2与双曲线的交点为A、B,且|AB|=
=1(a>0,b>0),直线x=2与双曲线的交点为A、B,且|AB|= ![]() .
.
(Ⅰ)求椭圆与双曲线的方程;
(Ⅱ)过点F2的直线l与椭圆交于M、N两点,交双曲线与P、Q两点,当△F1MN(F1为椭圆的左焦点)的内切圆的面积取最大值时,求△F1PQ的面积.
【答案】解:(Ⅰ)由已知得 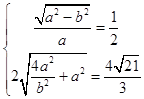 ,
,
解得a2=4,b2=3,
∴椭圆方程为 ![]() ,双曲线方程为
,双曲线方程为 ![]() =1.
=1.
(Ⅱ)∵三角形内切圆的半径与三角形周长的乘积是面积的2倍,且△F1MN的周长是定值8,
∴只需求出△F1MN面积的最大值.
设直线l方程为x=my+1,与椭圆方程联立得(3m2+4)y2+6my﹣9=0,
设M(x1 , y1),N(x2 , y2),则y1+y2=﹣ ![]() ,y1y2=﹣
,y1y2=﹣ ![]() ,
,
于是 ![]() =
= ![]() =
= ![]() =12
=12  .
.
∵ 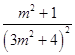 =
= 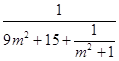 =
= 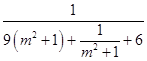 ≤
≤ ![]() ,
,
当且仅当m=0时,△F1MN(F1为椭圆的左焦点)的内切圆的面积取最大值,
∴△F1MN(F1为椭圆的左焦点)的内切圆的面积取最大值时,过点F2的直线l的方程为x=1,
联立 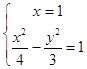 ,得P(1,
,得P(1, ![]() ),Q(1,﹣
),Q(1,﹣ ![]() ),F1(﹣1,0),
),F1(﹣1,0),
∴|PF1|=|QF1|= 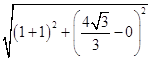 =
= ![]() ,|PQ|=
,|PQ|= ![]() ,|F1F2|=2,
,|F1F2|=2,
∴△F1PQ的面积S= ![]() =
= ![]() =
= ![]()
【解析】(Ⅰ)由已知得 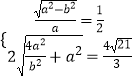 ,由此能求出椭圆和双曲线方程.(Ⅱ)设直线l方程为x=my+1,与椭圆方程联立得(3m2+4)y2+6my﹣9=0,由韦达定理和弦长公式推导出△F1MN(F1为椭圆的左焦点)的内切圆的面积取最大值时,过点F2的直线l的方程为x=1,由此能求出△F1PQ的面积.
,由此能求出椭圆和双曲线方程.(Ⅱ)设直线l方程为x=my+1,与椭圆方程联立得(3m2+4)y2+6my﹣9=0,由韦达定理和弦长公式推导出△F1MN(F1为椭圆的左焦点)的内切圆的面积取最大值时,过点F2的直线l的方程为x=1,由此能求出△F1PQ的面积.

练习册系列答案
相关题目