Question

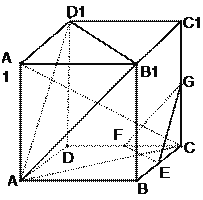
【题目】如图，在棱长为ɑ的正方体ABCD-A1B1C1D1中，E、F、G分别是CB、CD、CC1的中点．

（1）求直线C与平面ABCD所成角的正弦的值；

（2）求证：平面A B1D1∥平面EFG；

（3）求证：平面AA1C⊥面EFG ．

Answer 1

【答案】（1） ；（2）见解析；（3）见解析。

【解析】试题分析：(1)因为平面ABCD,所以为与平面ABCD所成角,

然后解三角形求出此角即可.

（2）证明面面平行根据判定定理只须证明平面平面A B1D1内两条相交直线和分别平行于平面EFG即可.在证明线面平行时又转化为证明线线平行.

(3)易证：BD平面AA1C，再证明EF//BD，因而可证出平面AA1C⊥面EFG.

（1）∵平面ABCD=C，在正方体ABCD-A1B1C1D1

平面ABCD

∴AC为在平面ABCD的射影

∴为与平面ABCD所成角……….2分

正方体的棱长为

∴AC=，=

………..4分

（2）在正方体ABCD-A1B1C1D1

连接BD，∥，=

为平行四边形

∴∥∵E，F分别为BC，CD的中点

∴EF∥BD∴EF∥…………3分

∵EF平面GEF，平面GEF

∴∥平面GEF …………7分

同理∥平面GEF∵=

∴平面A B1D1∥平面EFG ……………9分

（3）在正方体ABCD-A1B1C1D1∴平面ABCD

∵EF平面ABCD

∴EF …………10分

∵ABCD为正方形

∴ACBD

∵EF∥BD

∴ACEF ………..11分

∴EF平面AA1C

∵EF平面EFG

∴平面AA1C⊥面EFG …………….12分.