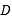题目内容
【题目】如图,三角形ABC的外接圆的O半径为![]() ,CD垂直于外接圆所在的平面,
,CD垂直于外接圆所在的平面, ![]()

(1)求证:平面![]()
![]() 平面
平面![]() .
.
(2)试问线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ?若存在,确定点
?若存在,确定点![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
【答案】(1)见解析;(2)满足条件的点M存在,且点M的坐标为![]() 。
。
【解析】试题分析:
(1)由题意结合几何关系可证得AC⊥BC,CD⊥BC,利用线面垂直的判断定理有BC⊥平面ACD,然后利用面面垂直的判断定理可得平面ADC![]() 平面BCDE
平面BCDE
(2)建立空间直角坐标系,结合题意可得满足条件的点M存在,且点M的坐标为![]() 。
。
试题解析:
(1)∵CD ⊥平面ABC,BE//CD
∴ BE⊥平面ABC,∴BE⊥AB
∵BE=1, ![]() ∴
∴ ![]() ,
,
从而![]()
∵⊙![]() 的半径为
的半径为![]() ,∴AB是直径,
,∴AB是直径,
∴AC⊥BC
又∵CD ⊥平面ABC,∴CD⊥BC,故BC⊥平面ACD
![]() 平面BCDE,∴平面ADC
平面BCDE,∴平面ADC![]() 平面BCDE
平面BCDE
(2)建立如图所示空间直角坐标系C—xyz,
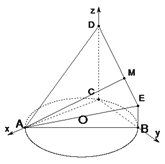
则:A(4,0,0),B(0,2,0),D(0,0,4),E(0,2,1),O(0,0,0),则![]()
易知平面ABC的法向量为![]() ,假设M点存在,设
,假设M点存在,设![]() ,则
,则![]() ,再设
,再设![]()
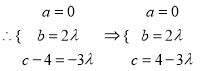 ,
,
即![]() ,从而
,从而![]() …10分
…10分
设直线BM与平面ABD所成的角为![]() ,则:
,则:
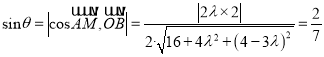
解得![]() ,其中
,其中![]() 应舍去,而
应舍去,而![]() 故满足条件的点M存在,且点M的坐标为
故满足条件的点M存在,且点M的坐标为![]()

练习册系列答案
相关题目