题目内容
 (2012•包头一模)如图,四边形DCBE为直角梯形,∠DCB=90°,DE∥CB,DE=1,BC=2,又AC=1,∠ACB=120°,CD⊥AB,直线AE与直线CD所成角为60°.
(2012•包头一模)如图,四边形DCBE为直角梯形,∠DCB=90°,DE∥CB,DE=1,BC=2,又AC=1,∠ACB=120°,CD⊥AB,直线AE与直线CD所成角为60°.(Ⅰ)求证:平面ACD⊥平面ABC;
(Ⅱ)求BE与平面ACE所成角的正弦值.
分析:(Ⅰ)证明CD⊥平面ABC,利用面面垂直的判定,可证平面ACD⊥平面ABC;
(Ⅱ)建立空间直角坐标系,用坐标表示点与向量,由直线AE与直线CD所成角为60°,确定
的坐标,求出平面ACE的一个法向量
=(
,3,-3),利用向量的夹角公式,可求BE与平面ACE所成角的正弦值.
(Ⅱ)建立空间直角坐标系,用坐标表示点与向量,由直线AE与直线CD所成角为60°,确定
| BE |
| n |
| 3 |
解答:(Ⅰ)证明:∵CD⊥AB,CD⊥CB,AB∩BC=B
∴CD⊥平面ABC
∵CD?平面ACD
∴平面ACD⊥平面ABC;
(Ⅱ)解:在平面ACB内,过C作CF⊥CB,以C为原点,以CF,CB,CD所在射线为x,y,z的正半轴建立空间直角坐标系C-xyz(如图)
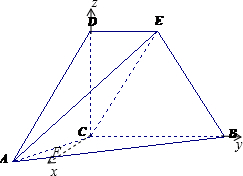
由题意,设CD=a(a>0),则D(0,0,a),E(0,1,a),B(0,2,0),A(
,-
,0)
∴
=(-
,
,a),
=(0,0,a)
由直线AE与直线CD所成角为60°,得
•
=|
||
|cos60°,即a2=
,解得a=1.
∴
=(0,1,1),
=(
,-
,0),
=(0,-1,1),
设平面ACE的一个法向量为
=(x,y,z),则
,
即
,取x=
,则y=3,z=-3,得
=(
,3,-3),
设BE与平面ACE所成角为θ,则sinθ=
=
,于是BE与平面ACE所成角的正弦值为
.
∴CD⊥平面ABC
∵CD?平面ACD
∴平面ACD⊥平面ABC;
(Ⅱ)解:在平面ACB内,过C作CF⊥CB,以C为原点,以CF,CB,CD所在射线为x,y,z的正半轴建立空间直角坐标系C-xyz(如图)

由题意,设CD=a(a>0),则D(0,0,a),E(0,1,a),B(0,2,0),A(
| ||
| 2 |
| 1 |
| 2 |
∴
| AE |
| ||
| 2 |
| 3 |
| 2 |
| CD |
由直线AE与直线CD所成角为60°,得
| AE |
| CD |
| AE |
| CD |
| a |
| 2 |
| a2+3 |
∴
| CE |
| CA |
| ||
| 2 |
| 1 |
| 2 |
| BE |
设平面ACE的一个法向量为
| n |
|
即
|
| 3 |
| n |
| 3 |
设BE与平面ACE所成角为θ,则sinθ=
|
| ||||
|
|
| ||
| 7 |
| ||
| 7 |
点评:本题考查面面垂直,考查线面角,考查利用空间向量解决立体几何问题,解题的关键是掌握面面垂直的判定方法,正确确定向量的坐标,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
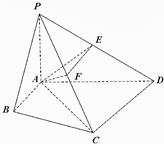 (2012•包头一模)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1.
(2012•包头一模)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1. (2012•包头一模)函数f(x)=sin(ωx+?)(其中
(2012•包头一模)函数f(x)=sin(ωx+?)(其中